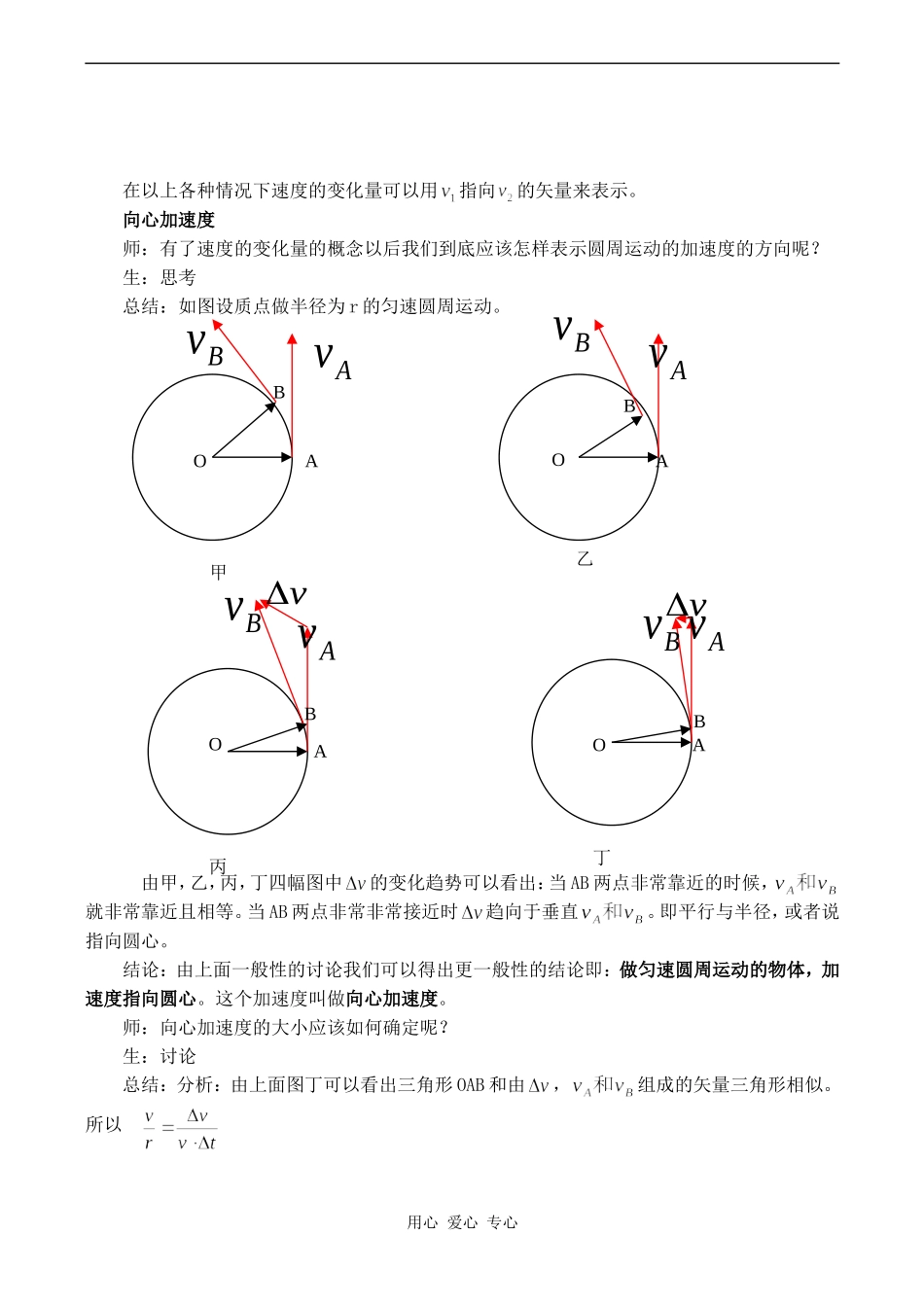
向心加速度知识与技能 1、理解速度变化量和向心加速度的概念。 2、知道向心加速度和线速度,角速度的关系。 3、能够用向心加速度公式求有关问题。 过程与方法体会用速度变化量的处理特点,体验向心加速度的导出过程,领会推导过程中用到的数学方法。情感态度价值观1、培养学生的思维能力和分析问题的能力,培养探究精神,感受成功的喜悦。重点难点重点:理解匀速圆周运动中产生加速度的原因,掌握向心加速度的确定方法和计算公式。 难点:向心加速度的方向的确定过程和其公式的推导过程。 教学方法 讲授、推理、归纳 教学过程设计引入:在前面的学习中我们已经了解到曲线运动是变速运动,有加速度。那么做圆周运动的物体的物体的加速度有何特点呢?由于加速度是矢量,所以既要考虑它的大小也要考虑它的方向。师问:做圆周运动的物体的加速度的方向应该是怎样的呢?下面我们通过两个具体问题来加以猜测(展示课本上 P48 页的两个例子)在例 2 中对小球进行受力分析可以发现小球的合力方向沿着细线的方向,可以作出的猜想是:圆周运动的物体的加速度可能沿着指向圆心的方向。但能不能讲任何圆周运动的方向都沿着指向圆心的方向呢?生:思考。。。总结:显然不可以,从两个例子我们不能得出普遍规律。要进行更严谨的数学论证。要搞清楚圆周运动的加速度的特点我们需要了解速度的变化量。速度的变化量如图:设质点用心 爱心 专心2v1vv1v2vv1v2vv2v1vv在以上各种情况下速度的变化量可以用指向的矢量来表示。向心加速度师:有了速度的变化量的概念以后我们到底应该怎样表示圆周运动的加速度的方向呢?生:思考总结:如图设质点做半径为 r 的匀速圆周运动。 由甲,乙,丙,丁四幅图中的变化趋势可以看出:当 AB 两点非常靠近的时候,就非常靠近且相等。当 AB 两点非常非常接近时趋向于垂直。即平行与半径,或者说指向圆心。结论:由上面一般性的讨论我们可以得出更一般性的结论即:做匀速圆周运动的物体,加速度指向圆心。这个加速度叫做向心加速度。师:向心加速度的大小应该如何确定呢?生:讨论总结:分析:由上面图丁可以看出三角形 OAB 和由,组成的矢量三角形相似。 所以 用心 爱心 专心OAvBvBAv丙OAvBvBAv丁OAvBvBA乙AvBvBAO甲进一步解出 由 可以导出向心加速度的表达式为把代入,可以推出或课堂练习1 下面关于向心加速度的说法中正确的是( )A 向心加速度越大,物体的速率变化越快。B 向心加速度的...