相位生成载波(PGC)调制与解调(包含MATLAB代码)VIP免费

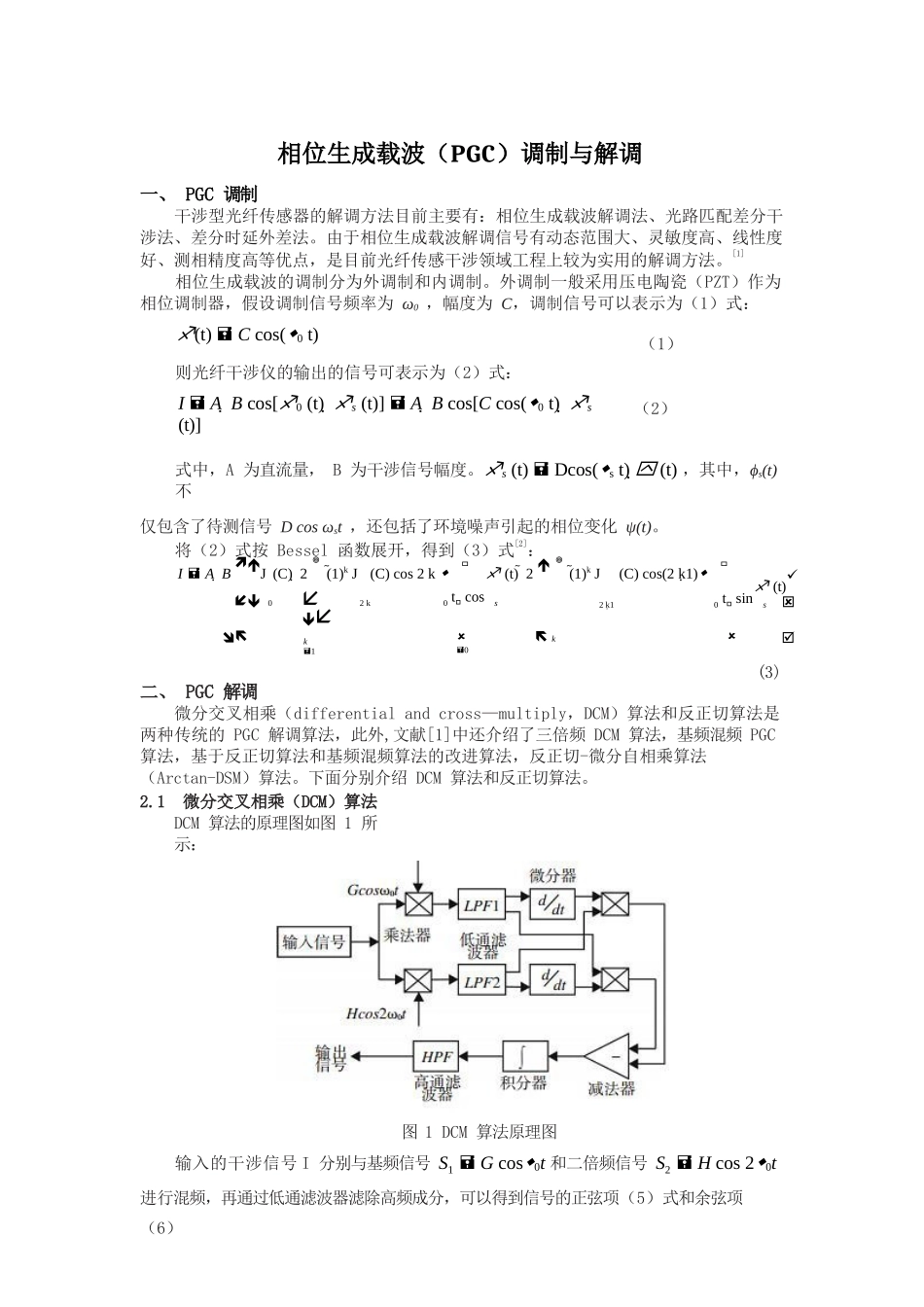
一、PGC调制相位生成载波（PGC）调制与解调干涉型光纤传感器的解调方法目前主要有：相位生成载波解调法、光路匹配差分干涉法、差分时延外差法。由于相位生成载波解调信号有动态范围大、灵敏度高、线性度好、测相精度高等优点，是目前光纤传感干涉领域工程上较为实用的解调方法。[1]相位生成载波的调制分为外调制和内调制。外调制一般采用压电陶瓷（PZT）作为相位调制器，假设调制信号频率为ω0，幅度为C，调制信号可以表示为（1）式：(t)Ccos(0t)则光纤干涉仪的输出的信号可表示为（2）式：IABcos[0(t)s(t)]ABcos[Ccos(0t)s(t)]（1）（2）式中，A为直流量，B为干涉信号幅度。s(t)Dcos(st)(t)，其中，ϕs(t)不仅包含了待测信号Dcosωst，还包括了环境噪声引起的相位变化ψ(t)。将（2）式按Bessel函数展开，得到（3）式[2]：IABJ(C)2(1)kJ(C)cos2k(t)2(1)kJ(C)cos(2k1)(t)02k0tcoss2k10tsins二、PGC解调k1k0(3)微分交叉相乘（differentialandcross—multiply，DCM）算法和反正切算法是两种传统的PGC解调算法，此外,文献[1]中还介绍了三倍频DCM算法，基频混频PGC算法，基于反正切算法和基频混频算法的改进算法，反正切-微分自相乘算法（Arctan-DSM）算法。下面分别介绍DCM算法和反正切算法。2.1微分交叉相乘（DCM）算法DCM算法的原理图如图1所示：图1DCM算法原理图输入的干涉信号I分别与基频信号S1Gcos0t和二倍频信号S2Hcos20t进行混频，再通过低通滤波器滤除高频成分，可以得到信号的正弦项（5）式和余弦项（6）12s12s12s12s式：I(t)BGJ1(C)sins(t)Q(t)BHJ2(C)coss(t)（5）（6）I(t)、Q(t)含有外界干扰，还不能直接提取待测信号，再通过微分交叉相乘（DCM）方法得到两个正交信号的平方项，利用sin2ϕs+cos2ϕs=1消除正交量，得到微分量（7）式：V'B2GHJ(C)J(C)'(t)(7)经过积分运算再通过高通滤波器滤除缓慢变化的环境噪声，最终得到的解调信号为得到（8）式：VB2GHJ(C)J(C)(t)B2GHJ(C)J(C)Dcos(t)(t)（8）相位噪声项ψ(t)通常情况下为缓变信号，将V通过高通滤波器滤除相位噪声，就可以得到待测信号，实现传感信号的解调（9）式。VoutB2GHJ(C)J(C)Dcos(t)(9)由式（9）可以看出，最后的解调输出信号与待测信号成线性关系，因此与后面将要讨论的反正切算法相比，产生的非线性失真要小的多。但是由于输出信号中的干涉幅度B=κA，而κ又与光传输中偏振态的变化有关，A是与光源光功率的稳定度、光路中各环节光功率的衰减、光纤干涉仪输入的光强等因素有关的量。因此，解调信号幅度受调制深度、光强、光路损耗、耦合器分光比、偏振态等诸多因素的影响。[1]2.2反正切算法反正切算法的原理如图2所示：图2反正切算法原理图反正切算法前端部分均与DCM法相同，只是该法在两路信号分别通过低通滤波器后，I(t)、Q(t)进行相除得到（10）式[3]：I(t)GJ1(C)tan(t)（10）sQ(t)HJ2(C)对式（10）进行反正切运算，得到（11）式：(t)Dcos(t)(t)arctan(I(t)*HJ2(C))（11）Q(t)*GJ1(C)噪声项ψ(t)通常情况下为缓变信号,通过高通滤波器滤除环境噪声ψ(t)即可得到待测信号Vout=Dcosωst。与DCM算法相比，反正切算法通过除法运算，消除了B对解调结果的影响，而且，如果令G=H,那么G、H对解调结果的影响也会被消除。同时，反正切算法比DCM算法原理相对简单，使得其解调算法比较简单，从而缩短了系统信号处理的时间，使系统的实时性得到了显著地提高。但是，由于调制深度（C值）的偏差，使得J1(C)/J2(C)不等于1，从而使解调结果产生了非线性，同时带来了严重的谐波失真以及总谐波失真。[1]C选取的原则是C的值尽可能小且使得J1(C）J2(C)的变化趋势趋于0。当C=2.37时，J1(C）J2(C)的导数为0，J1(C）J2(C)取得极大值。因此，对于PGC-DCM算法的最佳调制度C=2.37.而对于PGC-Arctan算法来讲，解调的结果是与J1(C）/J2(C)相关的。当C=2.63时，J1(C）/J2(C)=1，故对于传统的PGC-Arctan算法来讲，C=2.63是最佳调制度。无论是PGC-DCM算法还是PGC-...