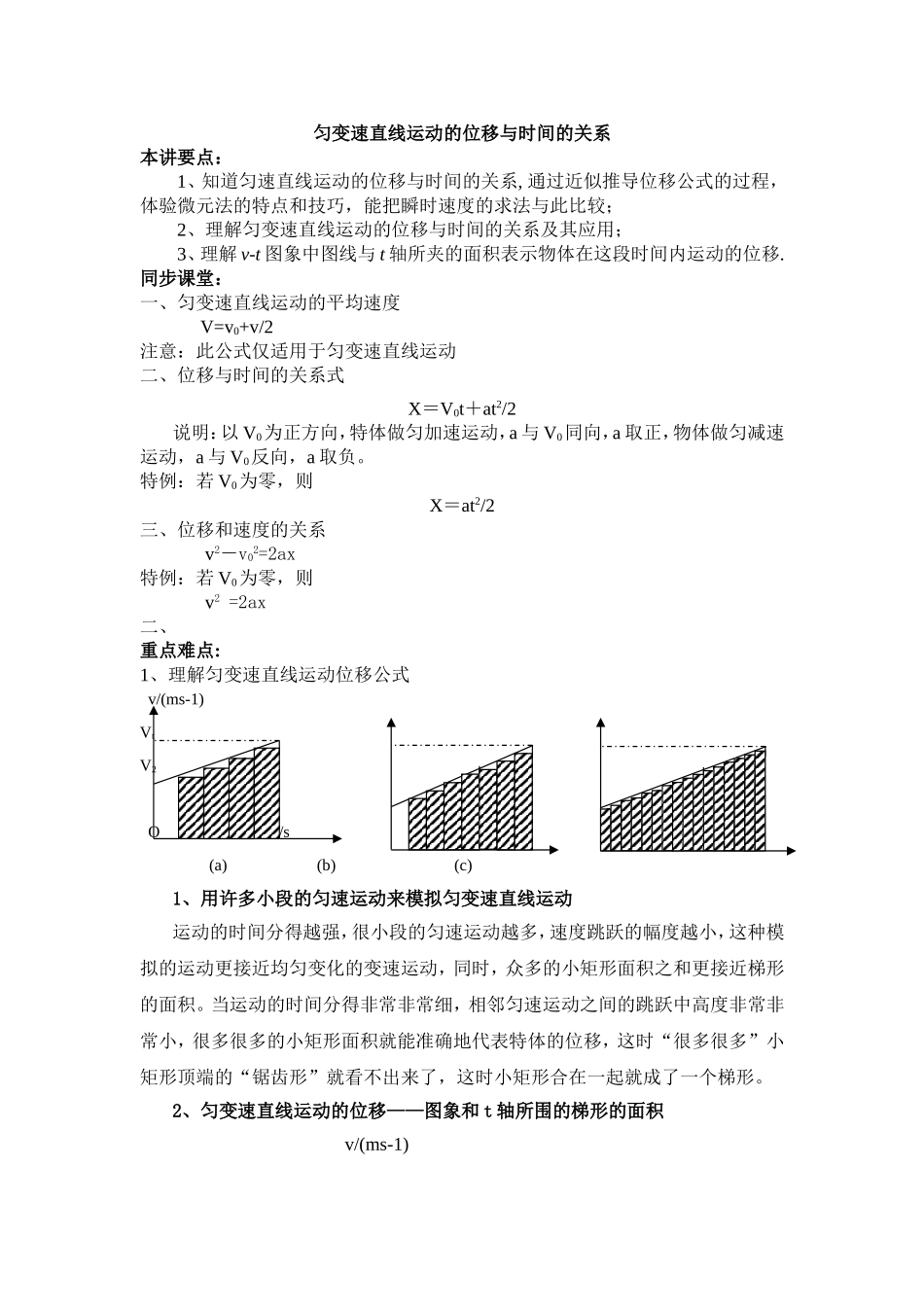
匀变速直线运动的位移与时间的关系本讲要点:1、知道匀速直线运动的位移与时间的关系, 通过近似推导位移公式的过程,体验微元法的特点和技巧,能把瞬时速度的求法与此比较;2、理解匀变速直线运动的位移与时间的关系及其应用;3、理解 v-t 图象中图线与 t 轴所夹的面积表示物体在这段时间内运动的位移.同步课堂:一、匀变速直线运动的平均速度 V=v0+v/2注意:此公式仅适用于匀变速直线运动二、位移与时间的关系式X=V0t+at2/2说明:以 V0为正方向,特体做匀加速运动,a 与 V0同向,a 取正,物体做匀减速运动,a 与 V0反向,a 取负。特例:若 V0为零,则X=at2/2三、位移和速度的关系 v2-v02=2ax特例:若 V0为零,则 v2 =2ax二、重点难点:1、理解匀变速直线运动位移公式 v/(ms-1)VtV2 O t t/s (a) (b) (c)1、用许多小段的匀速运动来模拟匀变速直线运动运动的时间分得越强,很小段的匀速运动越多,速度跳跃的幅度越小,这种模拟的运动更接近均匀变化的变速运动,同时,众多的小矩形面积之和更接近梯形的面积。当运动的时间分得非常非常细,相邻匀速运动之间的跳跃中高度非常非常小,很多很多的小矩形面积就能准确地代表特体的位移,这时“很多很多”小矩形顶端的“锯齿形”就看不出来了,这时小矩形合在一起就成了一个梯形。2、匀变速直线运动的位移——图象和 t 轴所围的梯形的面积 v/(ms-1) B C O A t/sx=(V0+Vt)·t(1) ——位移方程从(1)式可知,由 x= ·t, (2) 匀变速直线运动平均速度公式又由 V=V0+at(3) ——速度方程 x=V0t+at2(4) ——位移方程 又由(3)、(4)消去 t,V2-V 02=2ax(5) ——位移和速度关系方程 上述(1)、(3)、(4)、(5)四个方程均为矢量方程,每个方程均牵涉到四个物理量,在每个方程中,当知道其它三个量时,就可以求出第 4 个物理量,不过由于四个方程均可由其它两个方程导出,所以在一个过程中仅能解出两个未知数。典型例题:例题 1、火车沿平直铁轨匀加速前进,通过某一路标时的速度为 10.8km/h,L。1min 后变成 54km/h,再经一段时间,火车的速度达到 64 .8km/h。求所述过程中,火车的位移是多少?解法 1: 整个过程的平均速度m/s时间 t=75s则火车位移m解法 2: 由得位移m点拨①运动学公式较多,故同一个题目往往有不同求解方法;②为确定解题结果是否正确,用不同方法求解是一有效措施。例题 2、在平直公路上,一汽车的速度为 15m/s。,从某...