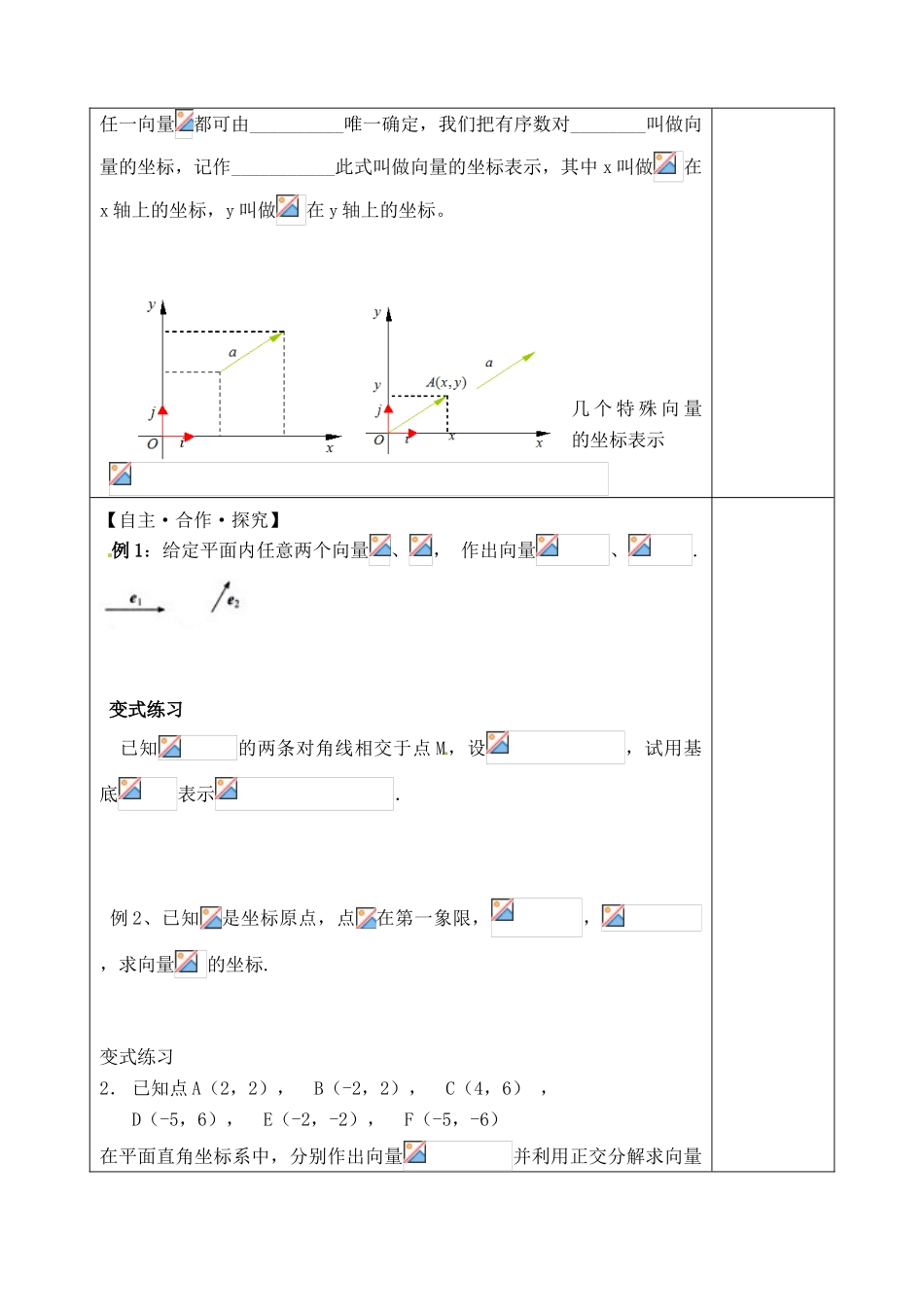
平面向量基本定理及坐标表示学习内容学习指导,即时感悟【使用说明及学法指导】1、回顾教材 P93-P96页,并思考课本上的思考及探究问题;2、在回顾教 材的基础上,完成导学案的【回顾·预习】与【自主·合作·探究】部分;3、找出自己的疑惑和需要讨论的问题准备课上讨论质疑。【学习目标】1.掌握平面向量基本定理,会判断两个向量能否组成一组基底;会将平面中的向量用基底表示。2.掌握平面向量的正交分解及其坐标表示.3.激情投入、合作探究、体会数学美。【学习重点】 平面向量基本定理,平面向量的正交分解及其坐标表示.【学习难点】 平面中的向量用基底或坐标表示【回顾·预习】1.平面向量的线性运算及其几何意义。2.平行向量基本定 理:____________________________________________________________________________________________.3.两向量的夹角与垂直::我们规定:已知两个非零向量,作,则 叫做向量与的夹角。如果则的取值范围是 。当 时,表示与同向;当 时,表示与反 向;当 时,表示与垂直。记作:.在不共线的两个向量中,,即两向量垂直是一种重要的情形,把一个向量分解为_ ____________,叫做把向量正 交分解。4、向量的坐标表示:在平面直角坐标系中,分别取与 x 轴、y 轴方向相同的两个_______作为基底。对于平面内的任一个向量,由平面向量基本定理可知,有且只有一对实数 x,y 使得____________,这样,平面内的任一向量都可由__________唯一确定,我们把有序数对________叫做向量的坐标,记作___________此式叫做向量的坐标表示,其中 x 叫做在x 轴上的坐标,y 叫做在 y 轴上的坐标。 几 个 特 殊 向 量的坐标表示【自主·合作·探究】 例 1:给定平面内任意两个向量、, 作出向量、.变式练习 已知的两条对角线相交于点 M,设,试用基底表示. 例 2、已知是坐标原点,点在第一象限,,,求向量的坐标. 变式练习2. 已知点 A(2,2), B(-2,2), C(4,6) , D(-5,6), E(-2,-2), F(-5,-6)在平面直角坐标系中,分别作出向量并利用正交分解求向量的坐标。【当堂达标】1.设 O 点是平行四边形 ABCD 两条对角线的交点,下列向量组中可作为这平行四边形所在的平面的基底的是( )(1)与;(2)与;(3)与;(4)与; A.(1)(2) B.(1)(3) C.(1)(4) D.(3)(4)2.在矩形 ABCD 中,O为两对角线交点,若 ,则( )A . B . C...