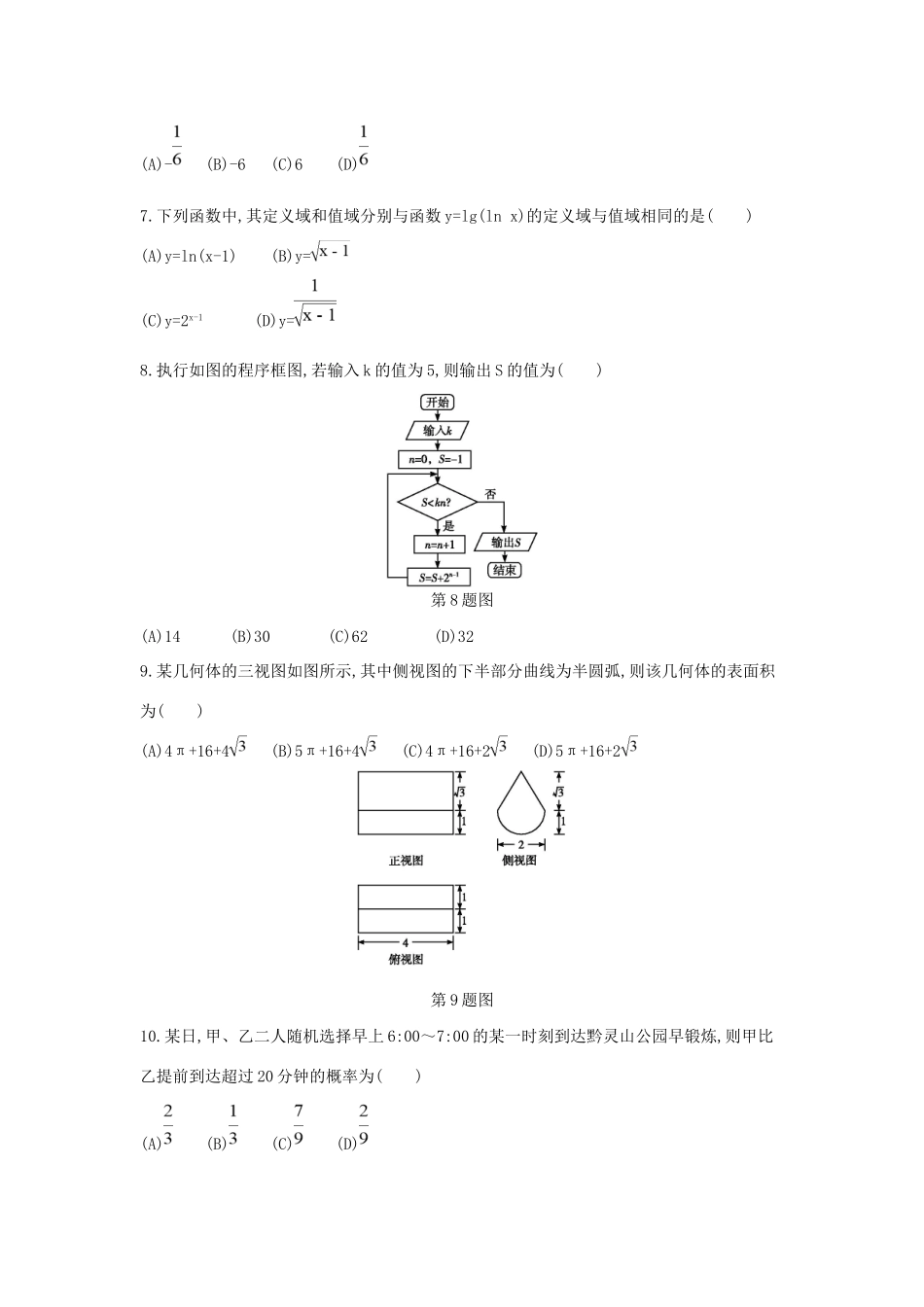
考前综合测评卷(一)(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合A={x|x-1≥0},集合B={x|2x-x2>0},则A∩B等于()(A)(0,2)(B)[-1,0)(C)[1,2)(D)⌀2.已知i是虚数单位,若a+bi=-(a,b∈R),则a+b的值是()(A)0(B)-i(C)-(D)3.f(x)=Asin(ωx+)(A,ω,为常数,A>0,ω>0,0<<π)的图象如图所示,则f()等于()(A)1(B)(C)(D)4.一直三棱柱的每条棱长都是3,且每个顶点都在球O的表面上,则球O的表面积为()(A)21π(B)24π(C)28π(D)36π5.已知抛物线x2=4y的焦点为F,其上有两点A(x1,y1),B(x2,y2)满足|AF|-|BF|=2,则y1+-y2-等于()(A)4(B)6(C)8(D)106.已知直线2mx-y-8m-3=0和圆C:(x-3)2+(y+6)2=25相交于A,B两点,当弦AB最短时,m的值为()(A)-(B)-6(C)6(D)7.下列函数中,其定义域和值域分别与函数y=lg(lnx)的定义域与值域相同的是()(A)y=ln(x-1)(B)y=(C)y=2x-1(D)y=8.执行如图的程序框图,若输入k的值为5,则输出S的值为()第8题图(A)14(B)30(C)62(D)329.某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为()(A)4π+16+4(B)5π+16+4(C)4π+16+2(D)5π+16+2第9题图10.某日,甲、乙二人随机选择早上6:00~7:00的某一时刻到达黔灵山公园早锻炼,则甲比乙提前到达超过20分钟的概率为()(A)(B)(C)(D)11.已知函数f(x)=sinωx-cosωx(ω>0)的图象的相邻两对称轴间的距离为,则当x∈[-,0]时,f(x)的最大值和单调增区间分别为()(A)1,[-,-](B)1,[-,-](C),[-,0](D),[-,0]12.已知函数g(x)=若方程g(x)-mx-m=0有且仅有两个不等的实根,则实数m的取值范围是()(A)(-,-2)∪[0,2](B)(-,-2]∪[0,2](C)(-,-2]∪[0,2)(D)(-,-2]∪[0,2)二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.设点P是△ABC所在平面内一点,且+=2,则+=.14.如图,△ABC及其内部的点组成的集合记为D,P(x,y)为D中任意一点,则z=2x+3y的最大值为.15.在锐角三角形中,角A,B,C的对边分别为a,b,c,若27(+)=104cosC,则=.16.刘老师带甲、乙、丙、丁四名学生去西安参加自主招生考试,考试结束后刘老师向四名学生了解考试情况.四名学生回答如下:甲说:“我们四人都没考好.”乙说:“我们四人中有人考得好.”丙说:“乙和丁至少有一人没考好.”丁说:“我没考好.”结果,四名学生中有两人说对了,则这四名学生中的两人说对了.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)若An和Bn分别表示数列{an}和{bn}的前n项的和,对任意正整数n,an=2(n+1),3An-Bn=4n.(1)求数列{bn}的通项公式;(2)记cn=,求{cn}的前n项和Sn.18.(本小题满分12分)如图是某市2月1日到14日的空气质量指数趋势图及空气质量指数与污染程度对应表.某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).空气质量指数污染程度小于100优良大于等于100且小于150轻度大于等于150且小于200中度大于等于200且小于300重度大于等于300且小于500严重大于等于500爆表(1)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)(2)求此人到达当日空气质量优良的概率;(3)求此人出差期间(两天)空气质量至少有一天为中度或重度污染的概率.19.(本小题满分12分)如图,在四棱锥AEFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF=2,四边形EFCB是高为的等腰梯形,EF∥BC,O为EF的中点.(1)求证:AO⊥CF;(2)求O到平面ABC的距离.20.(本小题满分12分)已知函数f(x)=+,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.(1)求a,b的值;(2)证明:当x>0,且x≠1时,f(x)>.21.(本小题满分12分)设直线l:y=k(x+1)(k≠0)与椭圆x2+3y2=a2(a>0)相交于两个不同的点A,B,与x轴相交于点C,记O为坐标原点.(1)证明:a2>;(2)若=2,求△OAB的面积取得最大值时的椭圆方程.请考生在第22~23题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)(选修44:坐标系与参数方程)已知曲线C的极坐标方程为ρ2=,直线l的参数方程为(t为参数).(1)求曲线C的直角坐标方程与直线l的普通方程;(2)若直线l交曲线C于M,N两点,求|MN|的值.23.(本小题满分10分)(选修45:不等式...