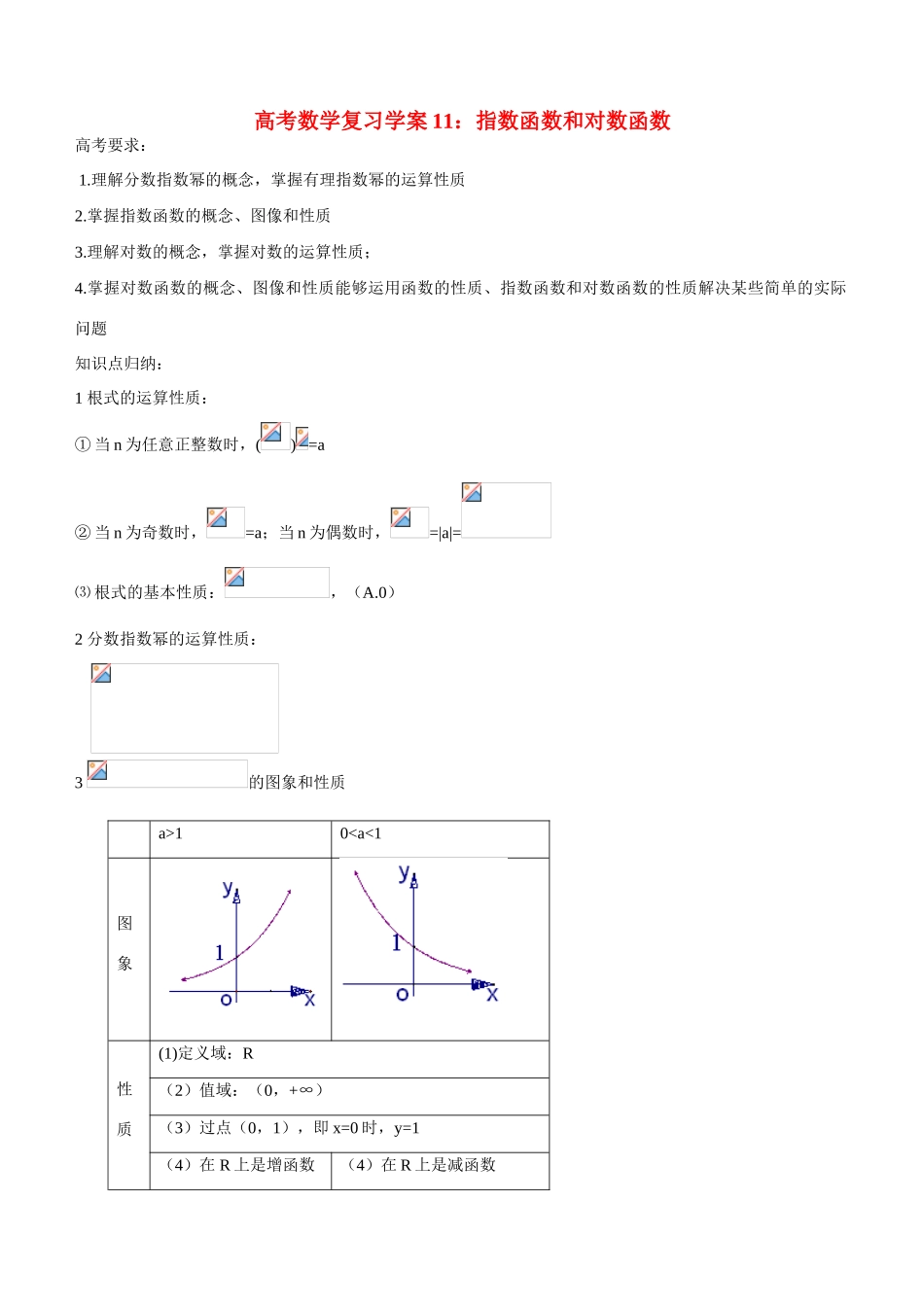
高考数学复习学案 11:指数函数和对数函数高考要求: 1.理解分数指数幂的概念,掌握有理指数幂的运算性质2.掌握指数函数的概念、图像和性质3.理解对数的概念,掌握对数的运算性质;4.掌握对数函数的概念、图像和性质能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题知识点归纳:1 根式的运算性质:① 当 n 为任意正整数时,() =a② 当 n 为奇数时,=a;当 n 为偶数时,=|a|=⑶ 根式的基本性质:,(A.0)2 分数指数幂的运算性质: 3 的图象和性质a>10
0 ,a 1 ,m > 0 ,m 1,N>0) 8.两个常用的推论:①, ② ( a, b > 0 且均不为 1)9.对数函数的性质:a>100.(转化法)af(x)=bg(x)f(x)logma=g(x)logmB.(取对数法)logaf(x)=logbg(x)logaf(x)=logag(x)/logab(换底法)题型讲解:例 1 计算:(1);(2); (3)解:(1)原式 (2)原式 (3)原式 例 2 已知,求的值解: ,∴,∴,∴, ∴,∴, 又 , ∴例 3 已知,且,求的值 解:由得:,即,∴; 同理可得,∴由 得 ,∴,∴, ,∴例 4 设,,且,求的最小值解:令 , ,,∴ 由得,∴, ∴, ,∴,即,∴, ∴, ,∴当时,例 5 设、、为正数,且满足 (1)求证: (2)若,,求、、的值证明:(1)左边;解:(2)由得,∴……………①由得………… ……………②由①②得……………………………………③由①得,代入得, , ∴………………………………④由③、④解得,,从而 例 6 (1)若,则,,从小到大依次为 ; (2)若,且,,都是正数,则,,从小到大依次为 ; (3)设,且(,),则与的大小关系是( ) A. B. C. D.解:(1)由得,故 (2)令,则,,,, ∴,∴;同理可得:,∴,∴(3...