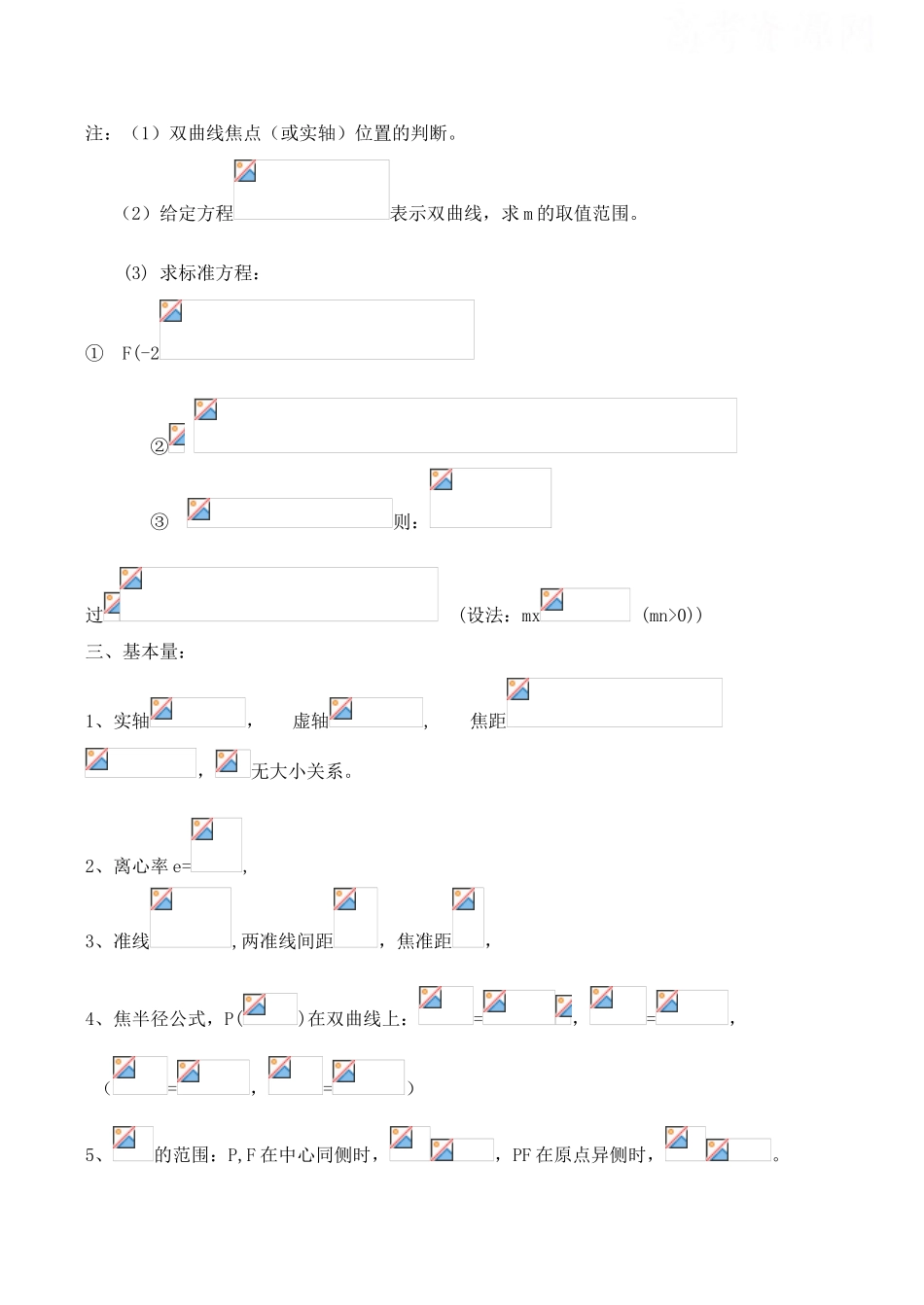
高考数学复习学案——圆锥曲线(双曲线)一、定义: 1、平面内,动点 P 到两定点 F1、F2 的距离之差的绝对值常数,,则 P 的运动轨迹是双曲线。其中 F1、F2 称为焦点,—实轴长,—焦距,—虚轴长注:1o、定义中无“绝对值”,则 P 的运动轨迹是双曲线的一支;2o、若,则 P 的运动轨迹是直线 F1F2上除去线段 F1F2 外的两条射线;3o、若,则 P 无运动轨迹。2、平面内,动点 P 到定点 F 的距离与到定直线 的距离之比,且,则 P 的运动轨迹是双曲线. 其中 F 为双曲线的一个焦点, 为与 F 相对应的准线,且焦准距例:1、双曲线,过左焦点 F1 作弦 PQ 交左支于 P、Q,且,求的周长。 (答案:) 2、双曲线上的 M 点到左焦点 F1 的距离为 5,求点 M 到右准线的距离。 (答案:,由于,故舍去 1,,再由第二定义,.) 3、过焦点 F2 作弦 PQ 交右支于 P、Q 两点,作,则由第二定义, 4、(1)F1(0,-3)、F2(0,3),,求 P 的轨迹方程; (2)F1(-1,0)、F2(3,0),,求 P 的轨迹方程;(答案:(1)(2))二、标准方程:1、以线段所在的直线为 x 轴,的中点为坐标原点,建立直角坐标系,则根据双曲线的定义或 =e = 均可推导出双曲线的标准方程: = 1 2、范围: (或),3、对称性:图像关于 x,y 轴分别对称,也关于原点中心对称。注:(1)双曲线焦点(或实轴)位置的判断。 (2)给定方程表示双曲线,求 m 的取值范围。 (3) 求标准方程:① F(-2 ② ③ 则: 过 (设法:mx (mn>0))三、基本量:1、实轴, 虚轴, 焦距,无大小关系。2、离心率 e=,3、准线,两准线间距,焦准距,4、焦半径公式,P()在双曲线上:=,=, (=,=)5、的范围:P,F 在中心同侧时,,PF 在原点异侧时,。6、参数方程:双曲线 ()上的点 P 可设为().7、过焦点 F 作双曲线的弦,若交同一支于 P,Q,则(通径) 若交不同支于 P,Q,则(实轴)8、中常利用:由此可推导出:=b,其中。四、双曲线特有的性质:渐近线1、双曲线,的渐近线方程为:求法:无需标准方程,只要令常数项为 0 即可反之,由渐近线方程可以设双曲线方程为特别地:当渐近线方程为时,双曲线称为等轴双曲线,可设为此种双曲线的离心率2 、 焦 点 F 到 渐 近 线的 距 离 为 b , 即 形 成 一 个 基 本 三 角 形, 其 中,此 H 恰好也是准线与渐近线的交点。3、过顶点作实轴的垂线,与渐近线,实轴围成一个三角形,由其可求离心率4、一条直线与双曲线只有一个公共点,有两种情形:1)与双曲线相切 2)与渐近线平行,故时常可采用数形结合的方法求直线的斜率的范围。