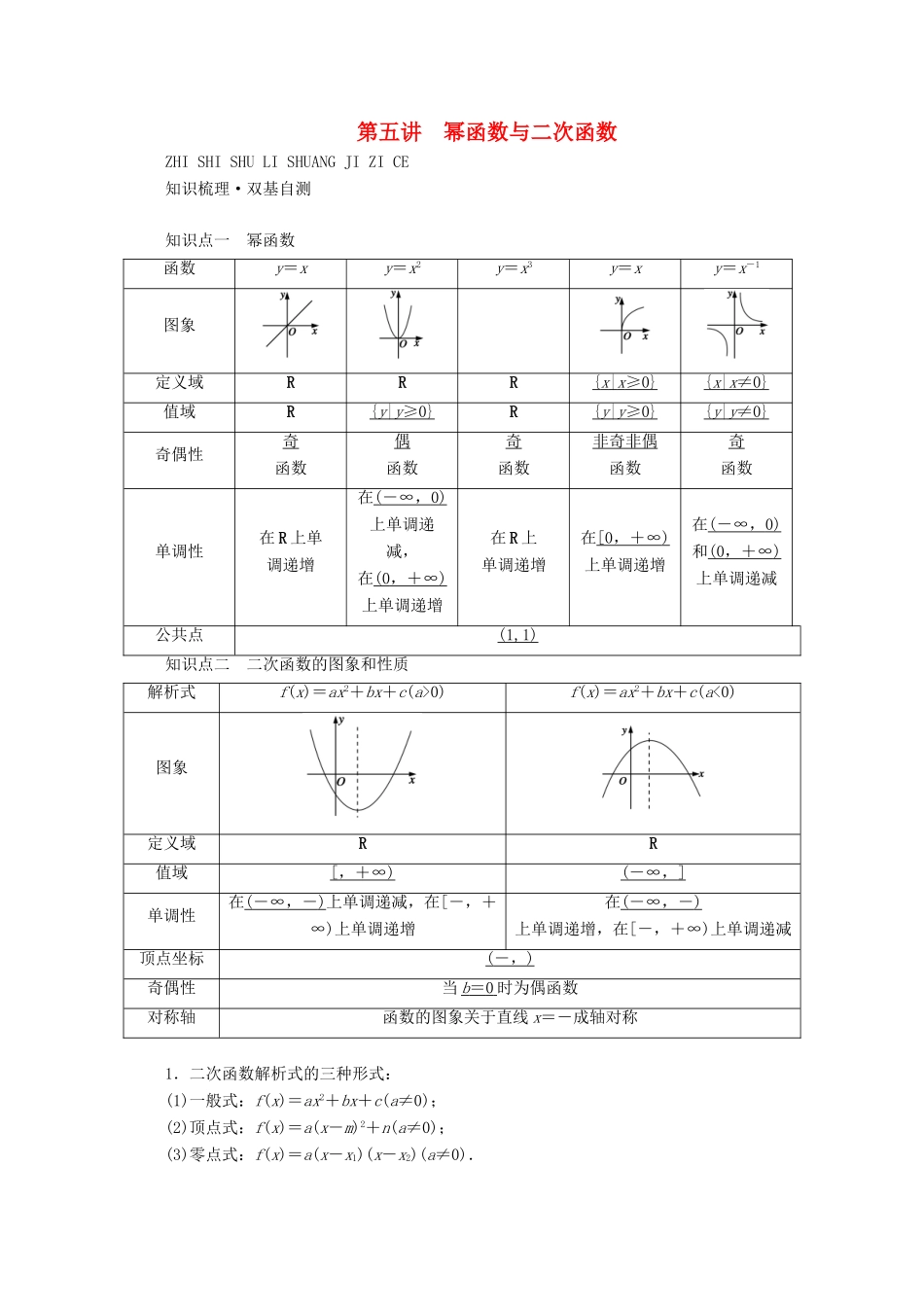
第五讲 幂函数与二次函数ZHI SHI SHU LI SHUANG JI ZI CE知识梳理·双基自测 知识点一 幂函数函数y=xy=x2y=x3y=xy=x-1图象定义域RRR{ x | x ≥0} { x | x ≠0} 值域R{ y | y ≥0} R{ y | y ≥0} { y | y ≠0} 奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性在 R 上单调递增在( -∞, 0) 上单调递减,在(0 ,+∞ ) 上单调递增在 R 上单调递增在[0 ,+∞ ) 上单调递增在( -∞, 0) 和(0 ,+∞ ) 上单调递减公共点(1,1)知识点二 二次函数的图象和性质解析式f(x)=ax2+bx+c(a>0)f(x)=ax2+bx+c(a<0)图象定义域RR值域[ ,+∞ ) ( -∞, ] 单调性在( -∞,- ) 上单调递减,在[-,+∞)上单调递增在( -∞,- ) 上单调递增,在[-,+∞)上单调递减顶点坐标( -, ) 奇偶性当 b = 0 时为偶函数对称轴函数的图象关于直线 x=-成轴对称1.二次函数解析式的三种形式:(1)一般式:f(x)=ax2+bx+c(a≠0);(2)顶点式:f(x)=a(x-m)2+n(a≠0);(3)零点式:f(x)=a(x-x1)(x-x2)(a≠0).2.一元二次不等式恒成立的条件:(1)“ax2+bx+c>0(a≠0)恒成立”的充要条件是“a>0,且 Δ<0”.(2)“ax2+bx+c<0(a≠0)恒成立”的充要条件是“a<0,且 Δ<0”.题组一 走出误区1.(多选题)下列结论中不正确的是( ABD )A.y=x0的图象是一条直线B.若幂函数 y=xn是奇函数,则 y=xn是增函数C.二次函数 y=ax2+bx+c(x∈R)不可能是奇函数D.当 n<0 时,幂函数 y=xn是定义域上的减函数题组二 走进教材2.(必修 1P79T1 改编)已知幂函数 f(x)=k·xα的图象过点(,),则 k+α=( C )A. B.1 C. D.2[解析] 由幂函数的定义知 k=1.又 f()=,所以()α=,解得 α=,从而 k+α=.3.(必修 1P39BT1 改编)函数 f(x)=-x2-6x+8,当 x=- 3 时,函数取得最大值 17.4.(必修 1P44AT9 改编)二次函数 y=f(x)满足 f(-1)=f(3),x1,x2是方程 f(x)=0 的两根,则 x1+x2=2.题组三 考题再现5.(2016·全国卷Ⅲ)已知 a=2,b=3,c=25,则( A )A.b
a>b.故选 A.6.(2017·浙江卷,5)若函数 f(x)=x2+ax+b 在区间[0,1]上的最大值是 M,最小值是m,则 M-m( B )A.与 a 有关,且与 b 有关 B.与...