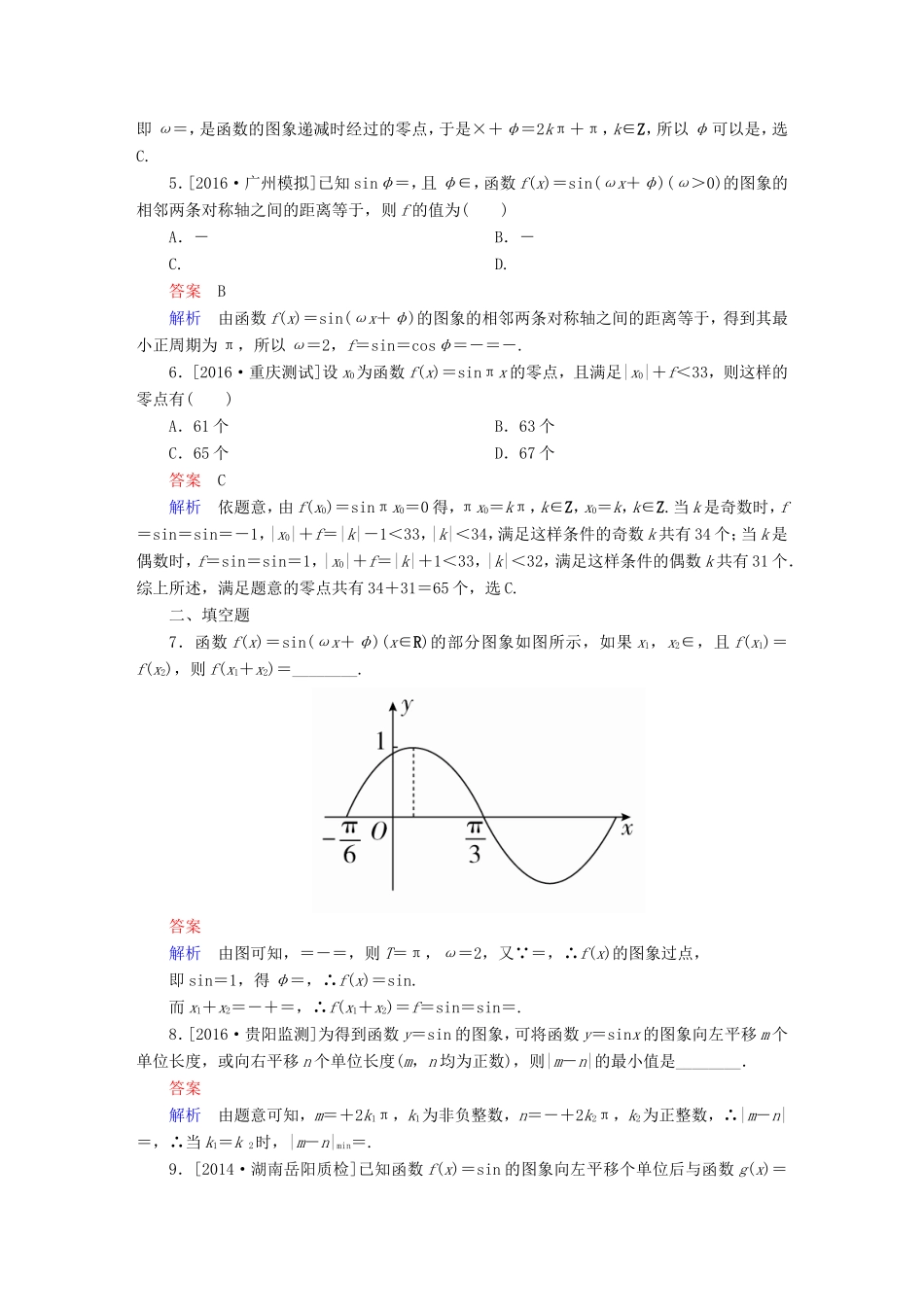
专题三三角函数与解三角形第一讲三角函数的图象与性质适考素能特训理一、选择题1.[2016·贵阳监测]下列函数中,以为最小正周期的奇函数是()A.y=sin2x+cos2xB.y=sinC.y=sin2xcos2xD.y=sin22x-cos22x答案C解析A中,y=sin2x+cos2x=sin,为非奇非偶函数,故A错;B中,y=sin=cos4x,为偶函数,故B错;C中,y=sin2xcos2x=sin4x,最小正周期为且为奇函数,故C正确;D中,y=sin22x-cos22x=-cos4x,为偶函数,故D错,选C.2.[2016·唐山统考]将函数y=cos2x-sin2x的图象向右平移个单位长度,所得图象对应的函数为g(x),则g(x)=()A.2sin2xB.-2sin2xC.2cosD.2sin答案A解析因为y=cos2x-sin2x=2sin=-2sin,将其图象向右平移个单位长度得到g(x)=-2sin=-2sin(2x-π)=2sin2x的图象,所以选A.3.[2016·武昌调研]已知函数f(x)=2sin-1(ω>0)的图象向右平移个单位后与原图象重合,则ω的最小值是()A.3B.C.D.答案A解析将f(x)的图象向右平移个单位后得到图象的函数解析式为2sin-1=2sin-1,所以=2kπ,k∈Z,所以ω=3k,k∈Z,因为ω>0,k∈Z,所以ω的最小值为3,故选A.4.[2016·沈阳质检]某函数部分图象如图所示,它的函数解析式可能是()A.y=sinB.y=sinC.y=sinD.y=-cos答案C解析不妨令该函数解析式为y=Asin(ωx+φ)(ω>0),由图知A=1,=-=,于是=,即ω=,是函数的图象递减时经过的零点,于是×+φ=2kπ+π,k∈Z,所以φ可以是,选C.5.[2016·广州模拟]已知sinφ=,且φ∈,函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于,则f的值为()A.-B.-C.D.答案B解析由函数f(x)=sin(ωx+φ)的图象的相邻两条对称轴之间的距离等于,得到其最小正周期为π,所以ω=2,f=sin=cosφ=-=-.6.[2016·重庆测试]设x0为函数f(x)=sinπx的零点,且满足|x0|+f<33,则这样的零点有()A.61个B.63个C.65个D.67个答案C解析依题意,由f(x0)=sinπx0=0得,πx0=kπ,k∈Z,x0=k,k∈Z.当k是奇数时,f=sin=sin=-1,|x0|+f=|k|-1<33,|k|<34,满足这样条件的奇数k共有34个;当k是偶数时,f=sin=sin=1,|x0|+f=|k|+1<33,|k|<32,满足这样条件的偶数k共有31个.综上所述,满足题意的零点共有34+31=65个,选C.二、填空题7.函数f(x)=sin(ωx+φ)(x∈R)的部分图象如图所示,如果x1,x2∈,且f(x1)=f(x2),则f(x1+x2)=________.答案解析由图可知,=-=,则T=π,ω=2,又 =,∴f(x)的图象过点,即sin=1,得φ=,∴f(x)=sin.而x1+x2=-+=,∴f(x1+x2)=f=sin=sin=.8.[2016·贵阳监测]为得到函数y=sin的图象,可将函数y=sinx的图象向左平移m个单位长度,或向右平移n个单位长度(m,n均为正数),则|m-n|的最小值是________.答案解析由题意可知,m=+2k1π,k1为非负整数,n=-+2k2π,k2为正整数,∴|m-n|=,∴当k1=k2时,|m-n|min=.9.[2014·湖南岳阳质检]已知函数f(x)=sin的图象向左平移个单位后与函数g(x)=sin的图象重合,则正数ω的最小值为________.答案解析将f(x)=sin的图象向左平移个单位后,得到函数f1(x)=sin的图象.又f1(x)=sin的图象与g(x)=sin的图象重合,故ωx+ω+=2kπ+ωx+,k∈Z.所以ω=12k-(k∈Z).又ω>0,故当k=1时,ω取得最小值,为12-=.三、解答题10.[2014·山东高考]已知向量a=(m,cos2x),b=(sin2x,n),函数f(x)=a·b,且y=f(x)的图象过点和点.(1)求m,n的值;(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象,若y=g(x)图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.解(1)由题意知f(x)=a·b=msin2x+ncos2x.因为y=f(x)的图象过点和,所以即解得(2)由(1)知f(x)=sin2x+cos2x=2sin.由题意知g(x)=f(x+φ)=2sin.设y=g(x)的图象上符合题意的最高点为(x0,2),由题意知x+1=1,所以x0=0,即到点(0,3)的距离为1的最高点为(0,2).将其代入y=g(x)得sin=1,因为0<φ<π,所以φ=,因此g(x)=2sin=2cos2x.由2kπ-π≤2x≤2kπ,k∈Z得kπ-≤x≤k...