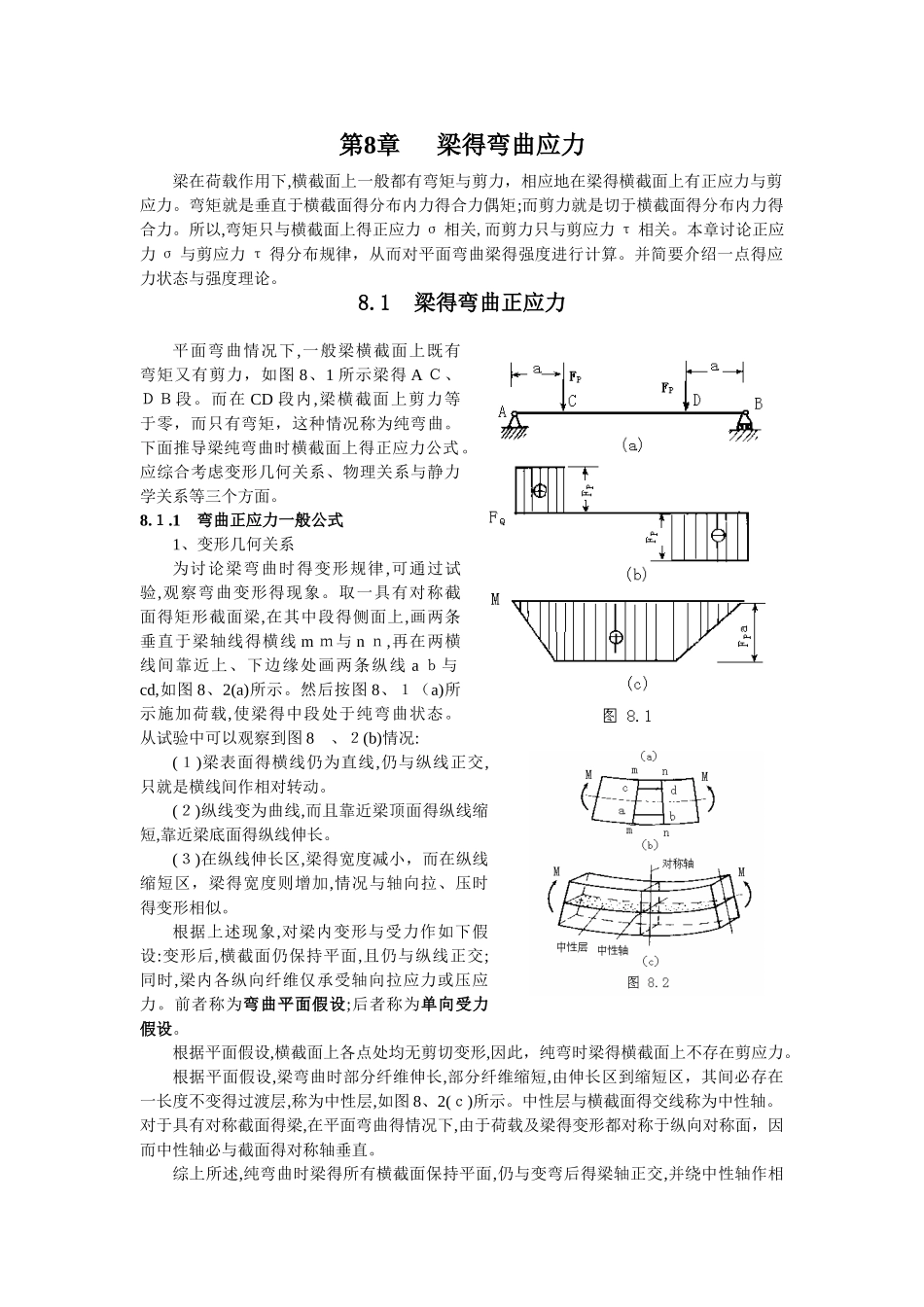
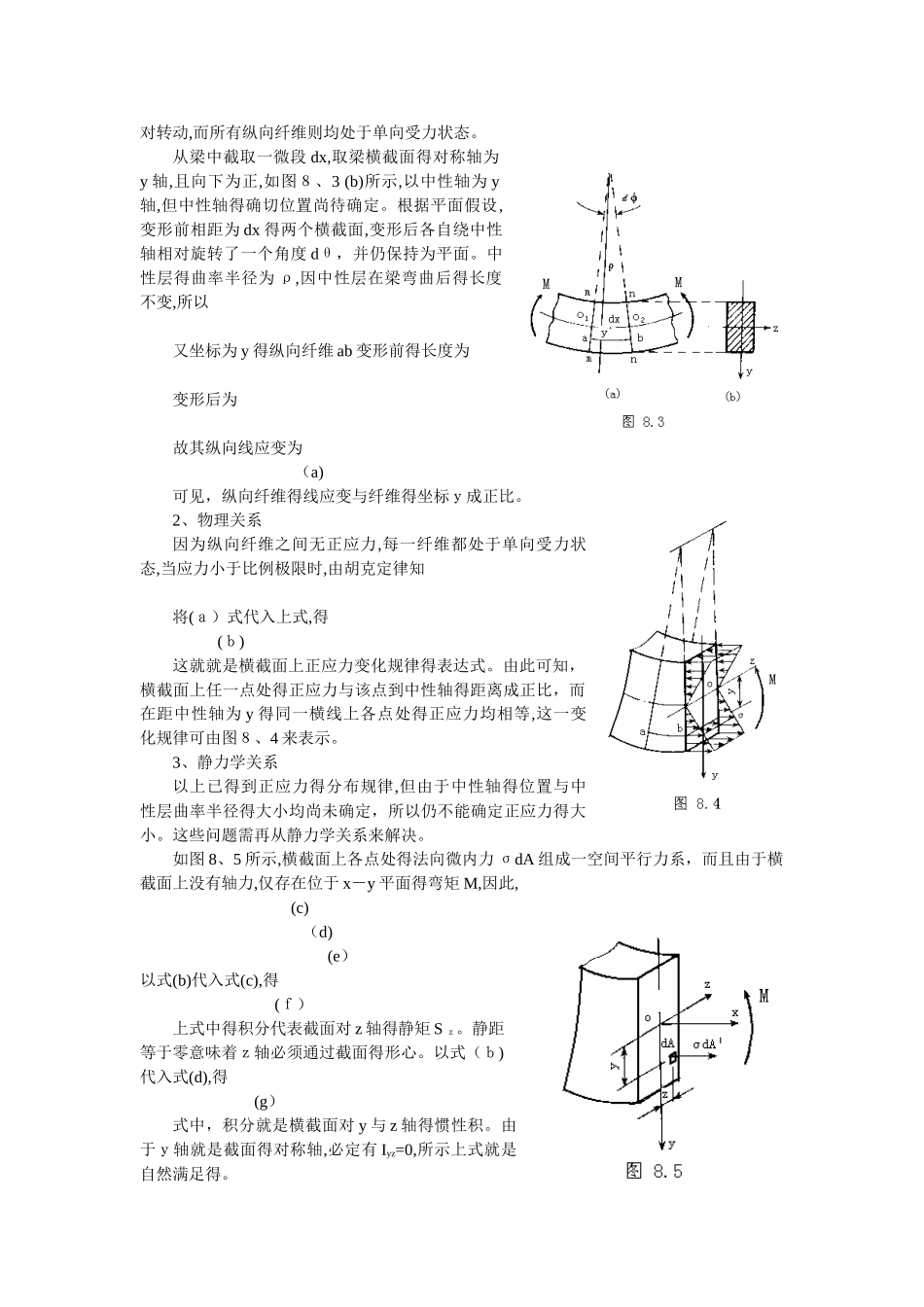
第8章梁得弯曲应力梁在荷载作用下,横截面上一般都有弯矩与剪力,相应地在梁得横截面上有正应力与剪应力。弯矩就是垂直于横截面得分布内力得合力偶矩;而剪力就是切于横截面得分布内力得合力。所以,弯矩只与横截面上得正应力 σ 相关,而剪力只与剪应力 τ 相关。本章讨论正应力 σ 与剪应力 τ 得分布规律,从而对平面弯曲梁得强度进行计算。并简要介绍一点得应力状态与强度理论。8.1梁得弯曲正应力平面弯曲情况下,一般梁横截面上既有弯矩又有剪力,如图 8、1 所示梁得 A C、DB段。而在 CD 段内,梁横截面上剪力等于零,而只有弯矩,这种情况称为纯弯曲。下面推导梁纯弯曲时横截面上得正应力公式。应综合考虑变形几何关系、物理关系与静力学关系等三个方面。8.1.1 弯曲正应力一般公式1、变形几何关系为讨论梁弯曲时得变形规律,可通过试验,观察弯曲变形得现象。取一具有对称截面得矩形截面梁,在其中段得侧面上,画两条垂直于梁轴线得横线 m m与 n n,再在两横线间靠近上、下边缘处画两条纵线 a b与cd,如图 8、2(a)所示。然后按图 8、1(a)所示施加荷载,使梁得中段处于纯弯曲状态。从试验中可以观察到图 8 、2(b)情况:(1)梁表面得横线仍为直线,仍与纵线正交,只就是横线间作相对转动。(2)纵线变为曲线,而且靠近梁顶面得纵线缩短,靠近梁底面得纵线伸长。(3)在纵线伸长区,梁得宽度减小,而在纵线缩短区,梁得宽度则增加,情况与轴向拉、压时得变形相似。根据上述现象,对梁内变形与受力作如下假设:变形后,横截面仍保持平面,且仍与纵线正交;同时,梁内各纵向纤维仅承受轴向拉应力或压应力。前者称为弯曲平面假设;后者称为单向受力假设。根据平面假设,横截面上各点处均无剪切变形,因此,纯弯时梁得横截面上不存在剪应力。根据平面假设,梁弯曲时部分纤维伸长,部分纤维缩短,由伸长区到缩短区,其间必存在一长度不变得过渡层,称为中性层,如图 8、2(c)所示。中性层与横截面得交线称为中性轴。对于具有对称截面得梁,在平面弯曲得情况下,由于荷载及梁得变形都对称于纵向对称面,因而中性轴必与截面得对称轴垂直。综上所述,纯弯曲时梁得所有横截面保持平面,仍与变弯后得梁轴正交,并绕中性轴作相对转动,而所有纵向纤维则均处于单向受力状态。从梁中截取一微段 dx,取梁横截面得对称轴为y 轴,且向下为正,如图8、3 (b)所示,以中性轴为 y轴,但中性轴得确切位置尚待确定。根据平面假设,变形前相距为 dx 得两个横截面,变形后各自...