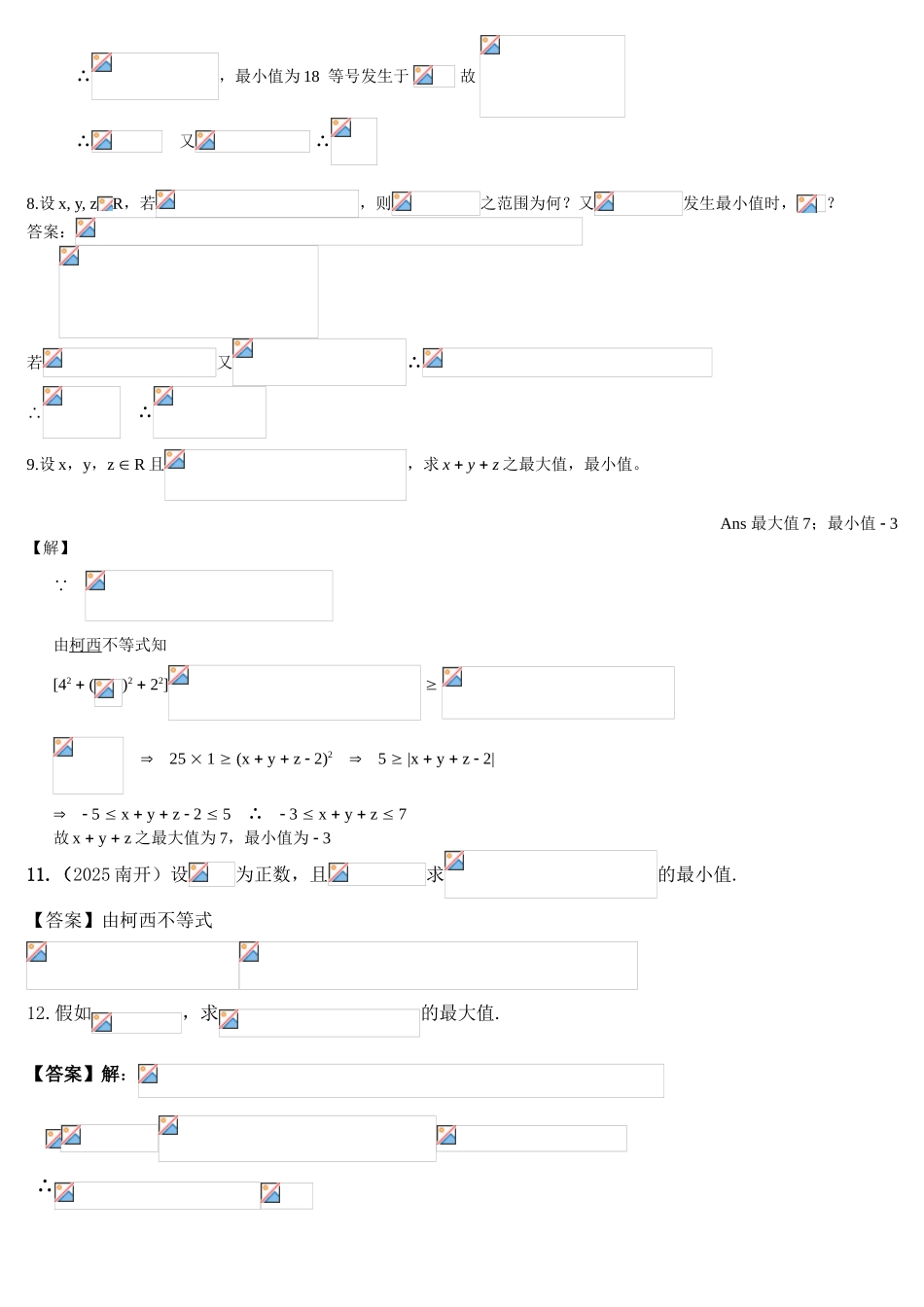
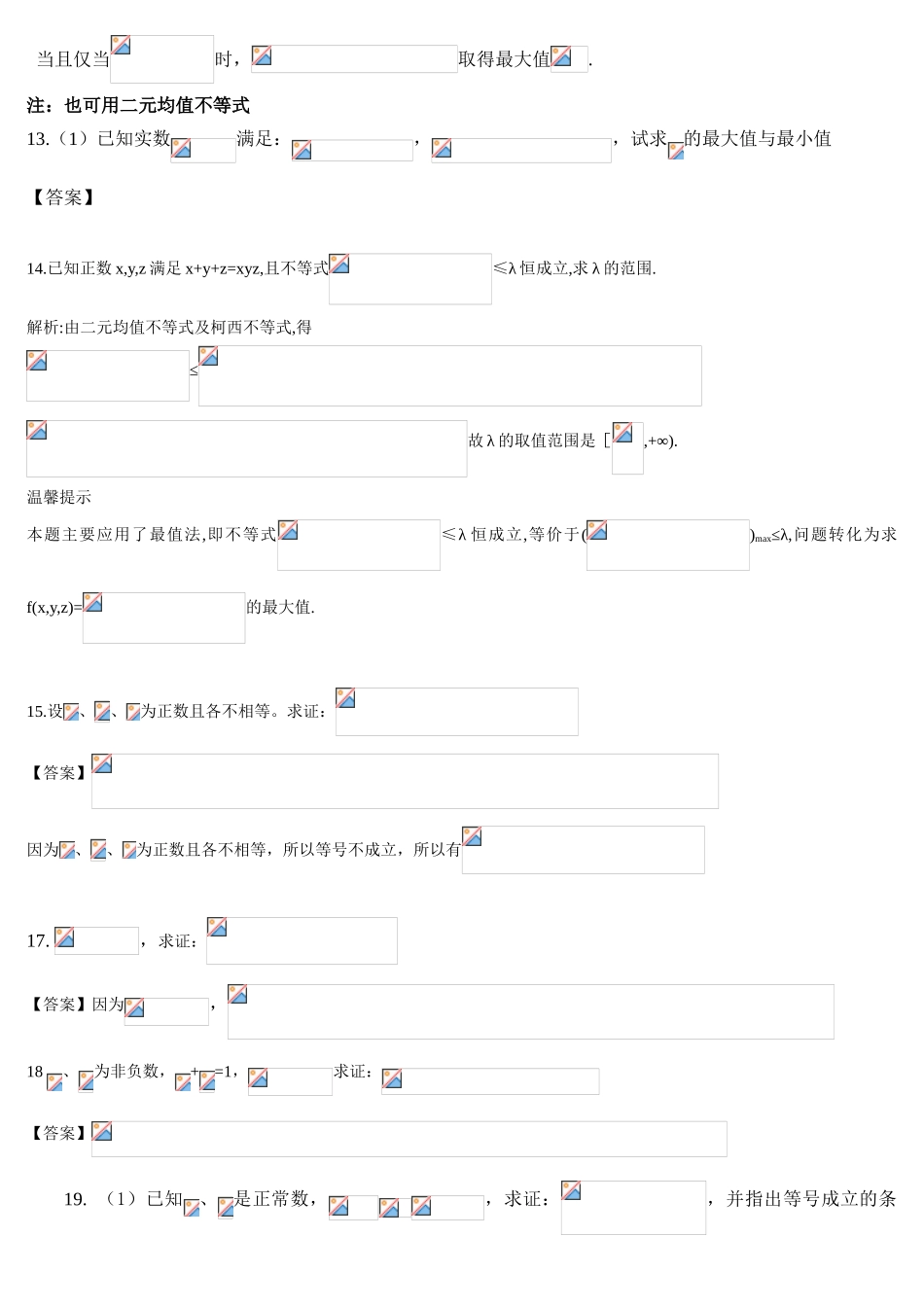
柯西不等式求最值 1. 设 a、b、c 为正数,求的最小值【答案】1212.设 x,y,z Î R,且满足 x2 + y2 + z2 = 5,则 x + 2y + 3z 之最大值为 解(x + 2y + 3z)2 £ (x2 + y2 + z2)(12 + 22 + 32) = 5.14 = 70∴ x + 2y + 3z 最大值为3.设 x,y,z Î R,若 x2 + y2 + z2 = 4,则 x - 2y + 2z 之最小值为 时,(x,y,z) = 解(x - 2y + 2z)2 £ (x2 + y2 + z2)[12 + ( - 2) 2 + 22] = 4.9 = 36∴ x - 2y + 2z 最小值为 - 6,公式法求 (x,y,z) 此时 ∴ ,,4.设,,试求的最大值 M 与最小值 m。答:根据柯西不等式 即 而有 故的最大值为 15,最小值为–15。5.设,试求之最小值即 将代入其中,得 而有 故之最小值为 4。变形:.设 x,y,z Î R,2x + 2y + z + 8 = 0,则(x - 1)2 + (y + 2)2 + (z - 3)2之最小值为[2(x - 1) + 2(y + 2) + (z - 3)]2 £ [(x - 1)2 + (y + 2) 2 + (z - 3) 2].(22 + 22 + 12)Þ (x - 1)2 + (y + 2) 2 + (z - 3) 2 ³= 96.设 x, y, zR,若,则之最小值为________,又此时________ ∴最小值 ∴ ∴7.设 a, b, c 均为正数,且,则之最小值为________,此时________。解: ∴,最小值为 18 等号发生于 故 ∴ 又 ∴8.设 x, y, zR,若,则之范围为何?又发生最小值时,?答案: 若又∴∴ ∴9.设 x,y,z Î R 且,求 x + y + z 之最大值,最小值。Ans 最大值 7;最小值 - 3【解】 由柯西不等式知[42 + ()2 + 22] ³ Þ 25 ´ 1 ³ (x + y + z - 2)2 Þ 5 ³ |x + y + z - 2|Þ - 5 £ x + y + z - 2 £ 5 ∴ - 3 £ x + y + z £ 7故 x + y + z 之最大值为 7,最小值为 - 311.(2025 南开)设为正数,且求的最小值.【答案】由柯西不等式12.假如,求的最大值. 【答案】解:∴当且仅当时,取得最大值.注:也可用二元均值不等式13.(1)已知实数满足:,,试求的最大值与最小值【答案】14.已知正数 x,y,z 满足 x+y+z=xyz,且不等式≤λ 恒成立,求 λ 的范围.解析:由二元均值不等式及柯西不等式,得≤故 λ 的取值范围是[,+∞).温馨提示本题主要应用了最值法,即不等式≤λ 恒成立,等价于()max≤λ,问题转化为求f(x,y,z)=的最大值.15...