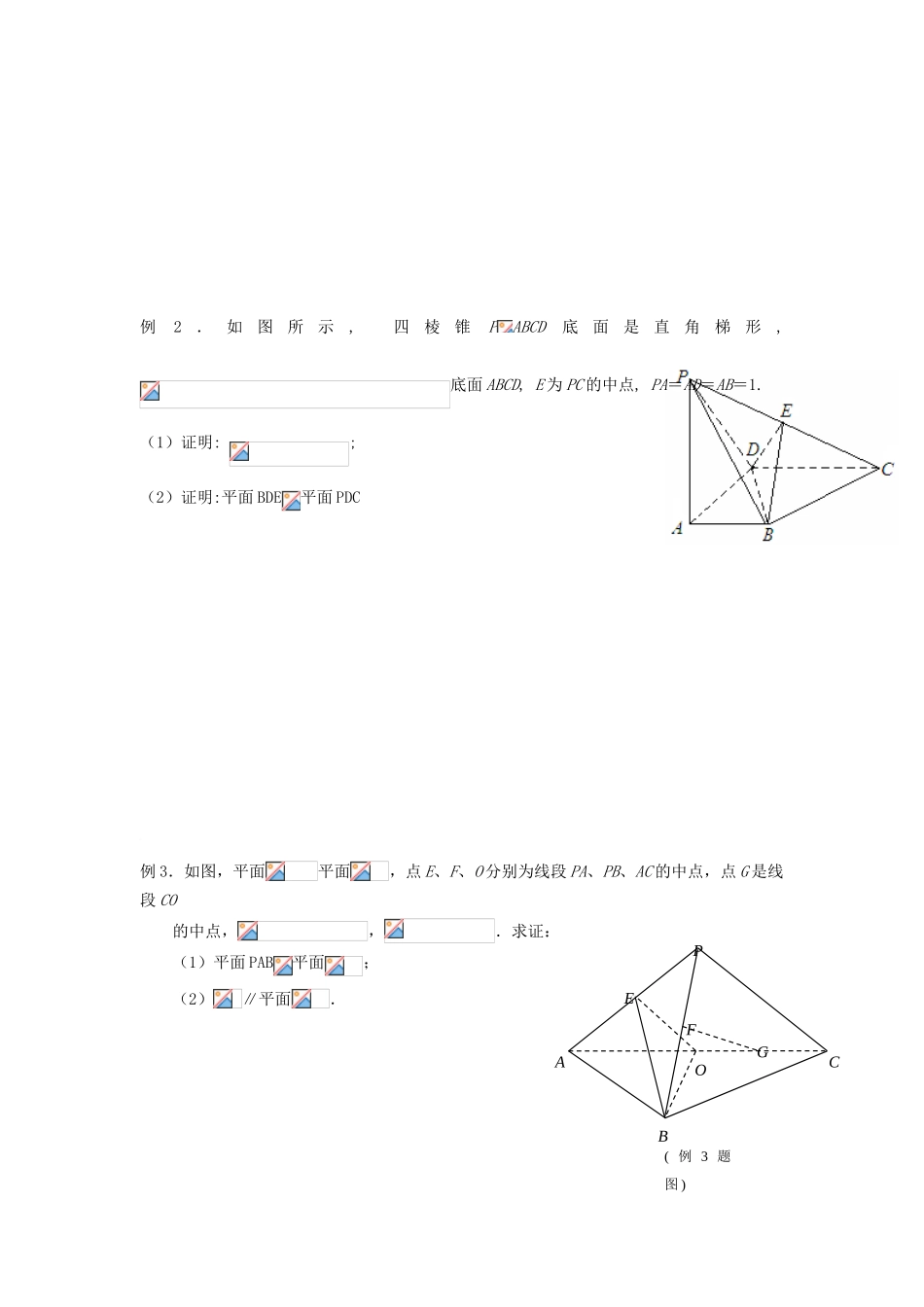
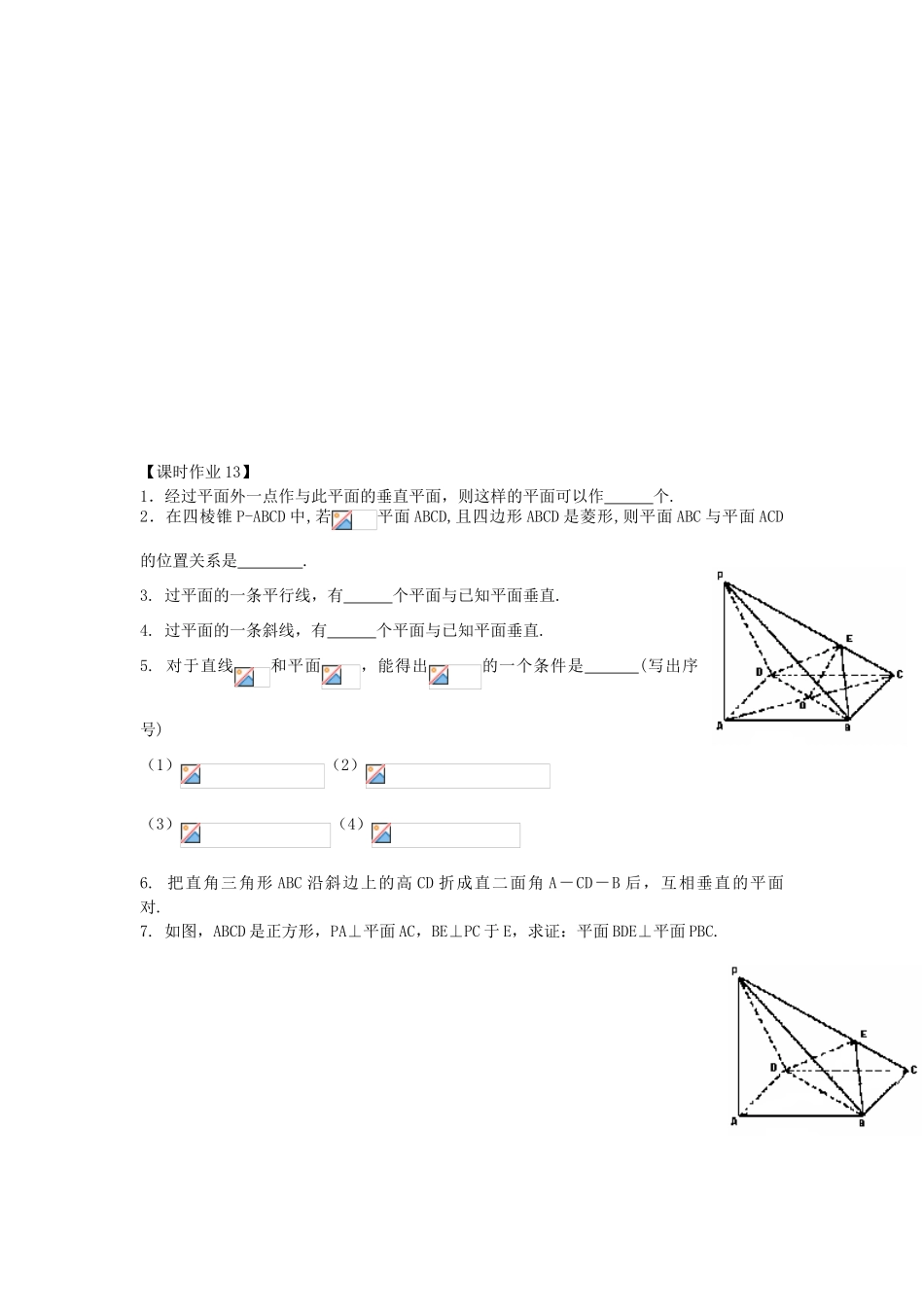
课时 13 两个平面垂直(2)【课标展示】1. 掌握平面与平面的位置关系.2.掌握平面和平面垂直的判定与性质定理.3. 应用平面和平面垂直的判定和性质定理证明线线垂直、线面垂直等有关问题.【先学应知】(一)要点1.平面与平面垂直的判定定理(1)语言表示:_________________________________________________________________________(2)符号表示:_________________________________________________________________________(3)图像表示: ________________________________________________________________________2.平面与平面垂直的性质定理(1)语言表示:_________________________________________________________________________(2)符号表示:_________________________________________________________________________(3)图像表示:________________________________________________________________【合作探究】例 1.如图,为空间四点.在中,.等边三角形以为轴运动.(Ⅰ)当平面平面时,求;(Ⅱ)当转动时,是否总有?证明你的结论.例2.如图所示, 四棱锥PABCD底面是直角梯形, 底面 ABCD, E 为 PC 的中点, PA=AD=AB=1. (1)证明: ;(2)证明:平面 BDE平面 PDC例 3.如图,平面平面,点 E、F、O 分别为线段 PA、PB、AC 的中点,点 G 是线段 CO的中点,,.求证:(1)平面 PAB平面;(2)∥平面.PABCOEFG( 例 3 题图 )【课时作业 13】1.经过平面外一点作与此平面的垂直平面,则这样的平面可以作 个.2.在四棱锥 P-ABCD 中,若平面 ABCD,且四边形 ABCD 是菱形,则平面 ABC 与平面 ACD的位置关系是 .3. 过平面的一条平行线,有 个平面与已知平面垂直.4. 过平面的一条斜线,有 个平面与已知平面垂直.5. 对于直线和平面,能得出的一个条件是 (写出序号)(1)(2)(3)(4)6. 把直角三角形 ABC 沿斜边上的高 CD 折成直二面角 A-CD-B 后,互相垂直的平面 对.7. 如图,ABCD 是正方形,PA⊥平面 AC,BE⊥PC 于 E,求证:平面 BDE⊥平面 PBC.8.如图,在正方体中,E、F 分别是、CD 的中点.求证:.9.(探究创新题)已知△BCD 中,∠BCD=90°,BC=CD=1,AB⊥平面 BCD,,E、F 分别是 AC、AD 上的动点,且求证:不论 λ 为何值,总有平面 BEF⊥平面 ABC.10.如图,在四棱锥 S-ABCD 中,底面 ABCD 为正方形,侧棱 SD⊥底面 ABCD,E、F...