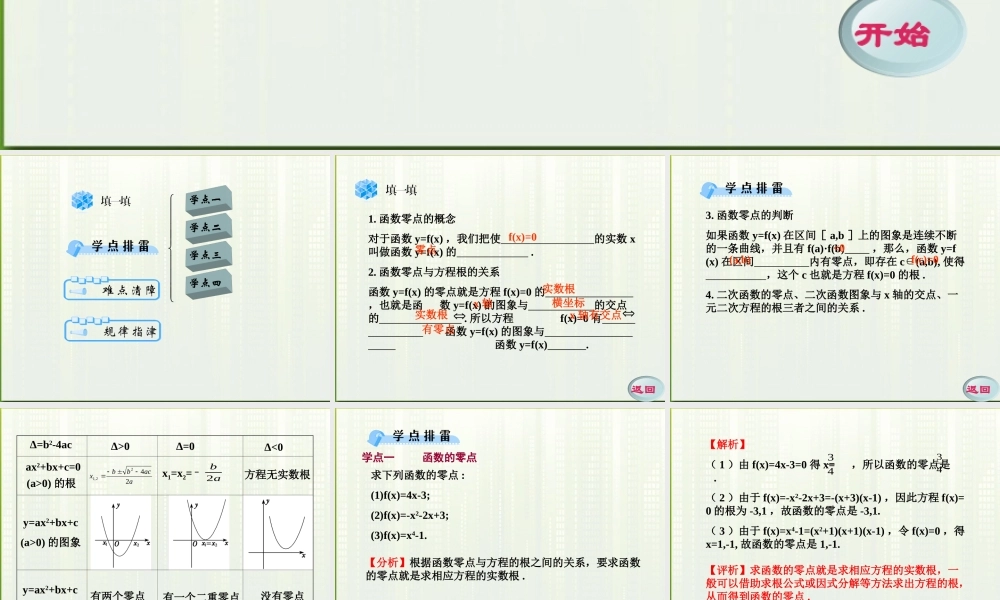
开始 学点一学点二学点三学点四 1. 函数零点的概念对于函数 y=f(x) ,我们把使 的实数 x叫做函数 y=f(x) 的 .2. 函数零点与方程根的关系函数 y=f(x) 的零点就是方程 f(x)=0 的 ,也就是函 数 y=f(x) 的图象与 的交点的 . 所以方程 f(x)=0 有 函数y=f(x) 的图象与 函数y=f(x) . f(x)=0零点实数根x 轴横坐标实数根x 轴有交点有零点返回 3. 函数零点的判断如果函数 y=f(x) 在区间[ a,b ]上的图象是连续不断的一条曲线,并且有 f(a)·f(b) ,那么,函数 y=f(x) 在区间 内有零点,即存在 c(a,b),∈使得 ,这个 c 也就是方程 f(x)=0 的根 .4. 二次函数的零点、二次函数图象与 x 轴的交点、一元二次方程的根三者之间的关系 .<0(a,b)f(c)=0返回 有两个零点Δ=b2-4acΔ>0Δ<0Δ=0ax2+bx+c=0(a>0) 的根y=ax2+bx+c(a>0) 的图象y=ax2+bx+c(a>0) 的零点方程无实数根x1=x2=ab2aacbbx2422,1有一个二重零点没有零点 返回 学点一 函数的零点求下列函数的零点 :(1)f(x)=4x-3;(2)f(x)=-x2-2x+3;(3)f(x)=x4-1.【分析】根据函数零点与方程的根之间的关系,要求函数的零点就是求相应方程的实数根 .返回 【解析】( 1 )由 f(x)=4x-3=0 得 x= ,所以函数的零点是 .( 2 )由于 f(x)=-x2-2x+3=-(x+3)(x-1) ,因此方程 f(x)=0 的根为 -3,1 ,故函数的零点是 -3,1.( 3 )由于 f(x)=x4-1=(x2+1)(x+1)(x-1) ,令 f(x)=0 ,得x=1,-1, 故函数的零点是 1,-1.4343【评析】求函数的零点就是求相应方程的实数根,一般可以借助求根公式或因式分解等方法求出方程的根,从而得到函数的零点 .返回 ( 1 )令 lnx-3=0, 得 x=e3,∴ 函数的零点为 x=e3.( 2 )方程 x3-7x+6=0 可化为x3-6x-x+6=x(x2-1)-6(x-1)=x(x+1)(x-1)-6(x-1) =(x-1)(x2+x-6)=(x-1)(x-2)(x+3)=0.即 (x-1)(x-2)(x+3)=0 得 x1=-3,x2=1,x3=2,∴ 函数 y=-x2-2x+3 的零点为 1,-3;函数 y=x3-7x+6 的零点为 -3,1,2.求下列函数的零点 :(1)y=lnx-3; (2)y=x3-7x+6.返回 学点二 判断零点判断函数 f(x)=x2-x-6 的零点是否存在,若存在 , 说明零点所在的一个区间 .【分析】要判断函数的零点的个数,实际就是考查方程 x2-x-6=0 的解的个数,即 y=x2-x-6 的图象与 x 轴的交点个数 .【解析】考查函数 f(x)=x2-x-6知图象为抛物线(如图所示),容易看出 ...