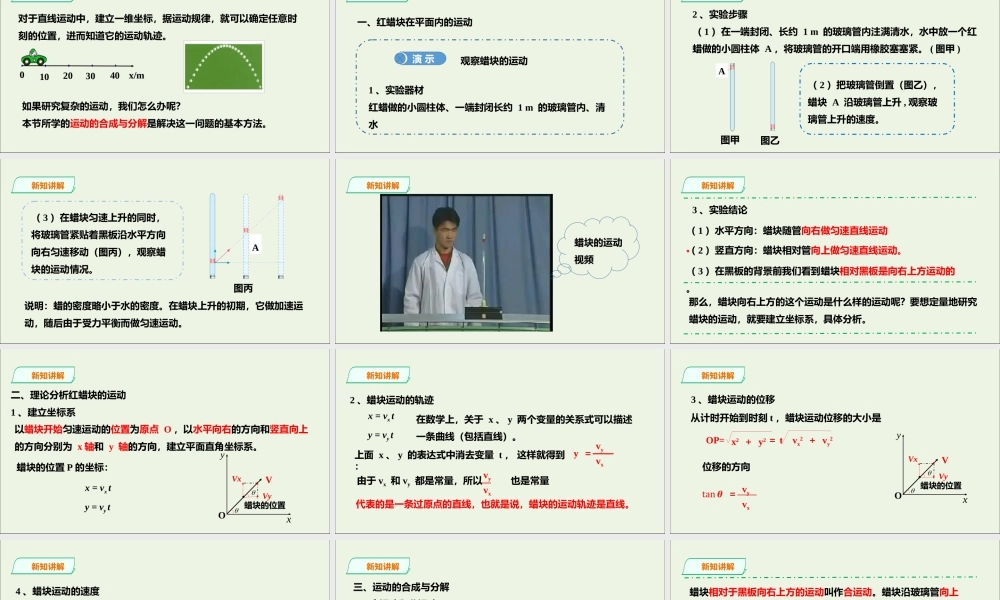
运动的合成与分解新知导入x/m030201040对于直线运动中,建立一维坐标,据运动规律,就可以确定任意时刻的位置,进而知道它的运动轨迹。如果研究复杂的运动,我们怎么办呢?本节所学的运动的合成与分解是解决这一问题的基本方法。新知讲解一、红蜡块在平面内的运动演 示观察蜡块的运动1 、实验器材红蜡做的小圆柱体、一端封闭长约 1 m 的玻璃管内、清水A新知讲解2 、实验步骤( 1 )在一端封闭、长约 1 m 的玻璃管内注满清水,水中放一个红蜡做的小圆柱体 A ,将玻璃管的开口端用橡胶塞塞紧。 ( 图甲 )( 2 )把玻璃管倒置(图乙),蜡块 A 沿玻璃管上升 , 观察玻璃管上升的速度。图甲图乙新知讲解( 3 )在蜡块匀速上升的同时,将玻璃管紧贴着黑板沿水平方向向右匀速移动(图丙),观察蜡块的运动情况。图丙A说明:蜡的密度略小于水的密度。在蜡块上升的初期,它做加速运动,随后由于受力平衡而做匀速运动。新知讲解蜡块的运动视频新知讲解3 、实验结论那么,蜡块向右上方的这个运动是什么样的运动呢?要想定量地研究蜡块的运动,就要建立坐标系,具体分析。( 1 )水平方向:蜡块随管向右做匀速直线运动。( 2 )竖直方向:蜡块相对管向上做匀速直线运动。( 3 )在黑板的背景前我们看到蜡块相对黑板是向右上方运动的。新知讲解二、理论分析红蜡块的运动1 、建立坐标系以蜡块开始匀速运动的位置为原点 O ,以水平向右的方向和竖直向上的方向分别为 x 轴和 y 轴的方向,建立平面直角坐标系。xy蜡块的位置VVxVyO蜡块的位置 P 的坐标:x = vx ty = vy t新知讲解2 、蜡块运动的轨迹x = vx ty = vy t在数学上,关于 x 、 y 两个变量的关系式可以描述一条曲线(包括直线)。y =——vxvy上面 x 、 y 的表达式中消去变量 t , 这样就得到:由于 vx 和 vy 都是常量,所以 也是常量 —vxvy代表的是一条过原点的直线,也就是说,蜡块的运动轨迹是直线。 新知讲解从计时开始到时刻 t ,蜡块运动位移的大小是3 、蜡块运动的位移位移的方向xy蜡块的位置VVxVyOvxvyOP= = t vx2 + vy2 x2 + y2新知讲解4 、蜡块运动的速度xy蜡块的位置VVxVyO如图所示:速度 v 与 vx 、 vy 的关系可根据勾股定理写出它们之间的关系:v = vx2 + vy2vxvy根据三角函数的知识新知讲解三、运动的合成与分解1 、合运动和分运动( 1 )合运动:物体实际的运动叫合运动...