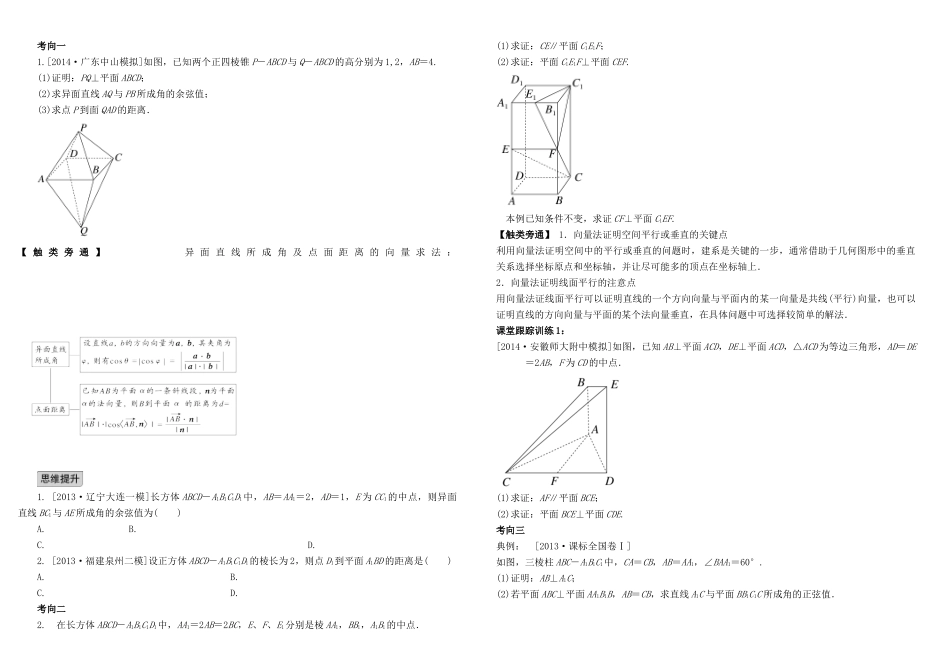
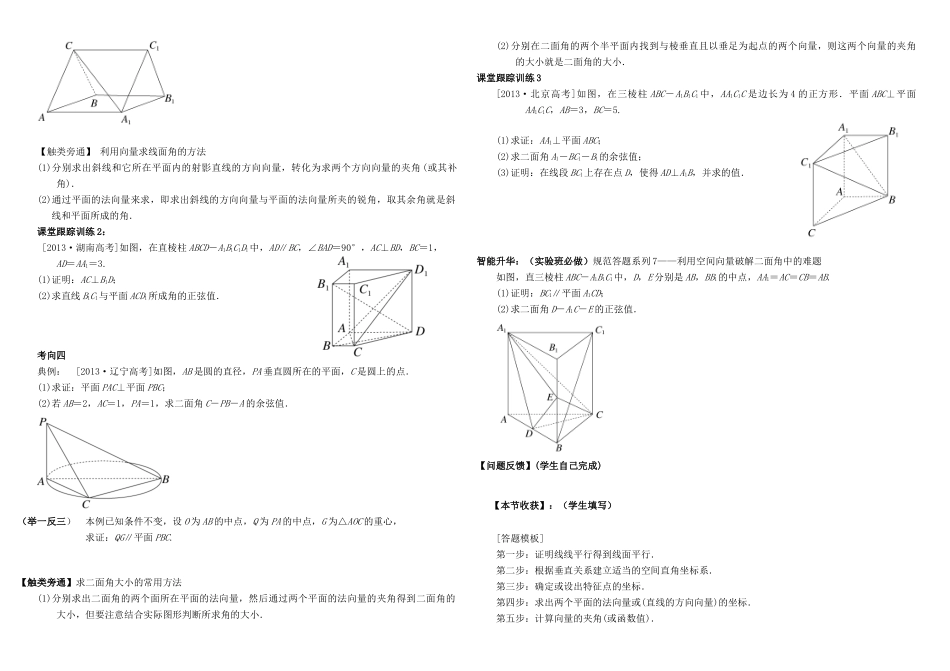
7-7 立体几何中的向量方法(自主学习)【学习目标】1.理解直线的方向向量与平面的法向量.2. 能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系.3. 能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理).4. 能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用.【学习任务】阅读选修 2-1 第 3 章第 2 节,完成以下内容一. 直线的方向向量和平面的法向量1.直线的方向向量直线 l 上的向量 e 或与 e 的向量叫做直线 l 的方向向量,显然一条直线的方向向量有 个.2.平面的法向量如果表示向量 n 的有向线段所在直线垂直于平面 α,则称这个向量垂直于平面 α,记作 n⊥α,此时向量 n 叫做平面 α 的法向量.显然一个平面的法向量也有 个,且它们是 向量.3.设直线 l,m 的方向向量分别为 a,b,平面 α,β 的法向量分别为 u,v,则l∥m⇔a∥b⇔a=kb,k∈R;l⊥m⇔a⊥b⇔a·b=0;l∥α⇔a⊥u⇔a·u=0;l⊥α⇔a∥u⇔a=ku,k∈R;α∥β⇔u∥v⇔u=kv,k∈R;α⊥β⇔u⊥v⇔u·v=0. 在求平面法向量时,所列方程组中有三个变量,但只有两个方程,如何处理? 下列命题是否正确(请在括号内填“√”或“×”).(1)若 n1,n2分别是平面 α、β 的法向量,则 n1∥n2⇔α∥β.( )(2)若 n1,n2分别是平面 α、β 内的向量,则 α∥β⇔n1∥n2.( )(3)若 n1是直线 l 的一个方向向量,n2是平面 α 的一个法向量,则 l∥α⇔n1⊥n2.( )(4)若 n1=(-7,3,4),n2=(x,y,8)分别是两直线 l1、l2的方向向量,若 l1∥l2,则 x+y=-8.( )二. 空间向量与空间角的关系1.两条异面直线所成角的求法设两条异面直线 a,b 的方向向量分别为 a,b,其夹角为 θ,则 cosφ=|cosθ|= (其中 φ为异面直线 a,b 所成的角).范围是(0,].2.直线和平面所成角的求法如图所示,设直线 l 的方向向量为 e,平面 α 的法向量为 n,直线 l 与平面 α 所成的角为 φ,两向量 e 与 n 的夹角为 θ,则有 sinφ=|cosθ|= .取值范围是[0,].3.求二面角的大小(1)如图①,AB、CD 是二面角 α-l-β 的两个半平面内与棱 l 垂直的直线,则二面角的大小 θ= .(2)如图②③,n1,n2分别是二面角 α-l-β 的两个半平面 α,β 的法向量,则二面角的大小 θ满足 cosθ=cos〈n1...