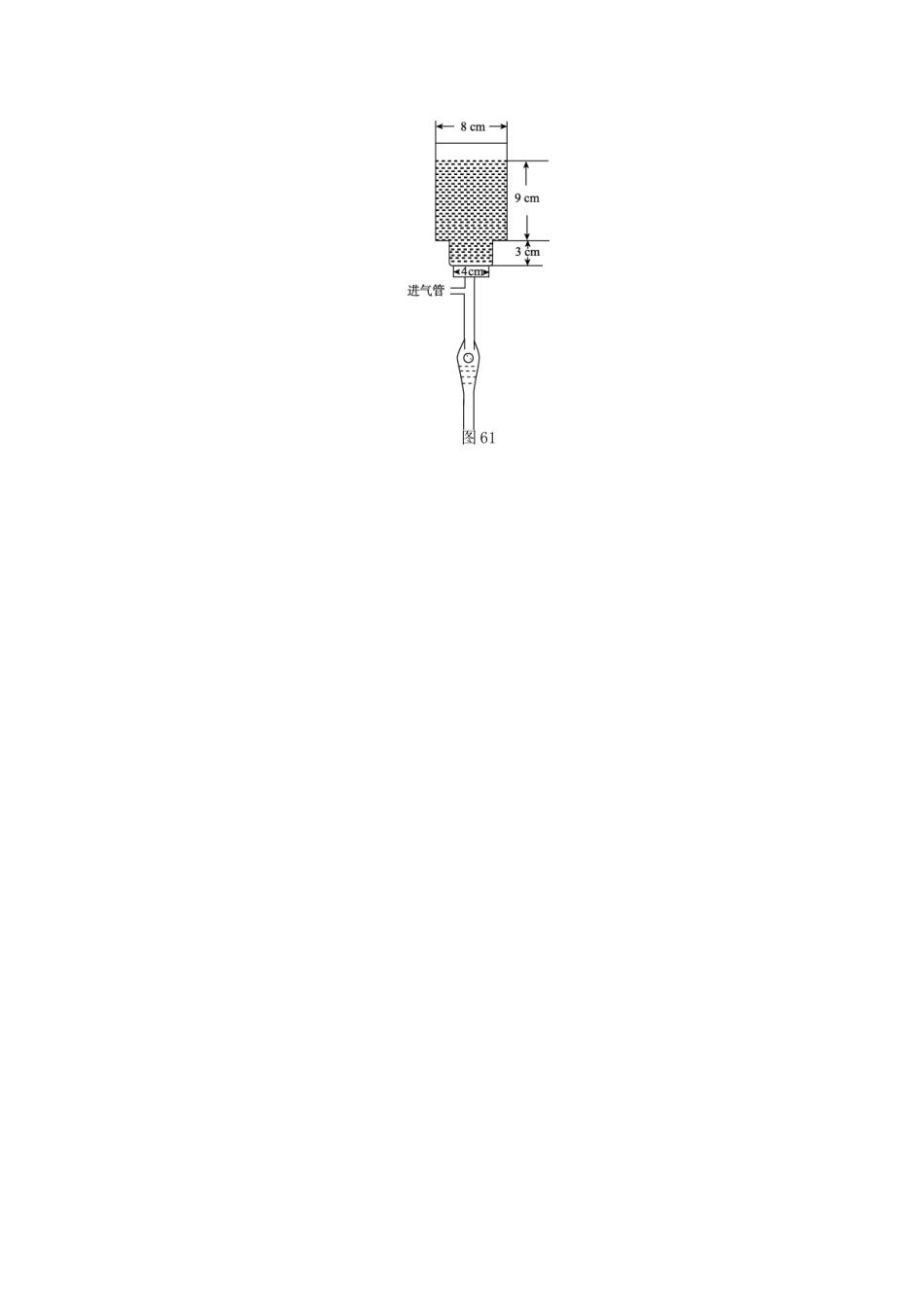
专题限时集训(六)[函数与方程、函数模型及其应用](时间:5分钟+40分钟)基础演练夯知识1.“m<0”是“函数f(x)=m+log2x(x≥1)存在零点”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.函数f(x)=2x+4x-3的零点所在的区间是()A.B.C.D.3.函数f(x)=tanx-在区间内零点的个数是()A.0B.1C.2D.34.已知f(x+1)=f(x-1),f(x)=f(-x+2),方程f(x)=0在[0,1]内有且只有一个根x=,则f(x)=0在区间[0,2013]内根的个数为()A.2011B.1006C.2013D.10075.若函数f(x)=ax+b的零点为x=2,则函数g(x)=bx2-ax的零点是x=0和x=________.提升训练强能力6.已知函数f(x)=则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是()A.[0,1)B.(-∞,1)C.(-∞,0]∪(1,+∞)D.(-∞,1]∪(2,+∞)7.已知函数f(x)是定义域为R的奇函数,且当x≤0时,f(x)=2x-x+a,则函数f(x)的零点的个数是()A.1B.2C.3D.48.已知函数f(x)=4-ax,g(x)=4-logbx,h(x)=4-xc的图像都经过点P,若函数f(x),g(x),h(x)的零点分别为x1,x2,x3,则x1+x2+x3=()A.B.C.D.9.若直角坐标平面内的两个不同的点P,Q满足条件:①P,Q都在函数y=f(x)的图像上;②P,Q关于原点对称.则称点对[P,Q]是函数y=f(x)的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”).已知函数f(x)=则此函数的“友好点对”有()A.0对B.1对C.2对D.3对10.若关于x的方程--kx-1=0有五个互不相等的实根,则k的取值范围是()A.B.∪C.∪D.∪11.已知f(x)=(x∈R),若关于x的方程f2(x)-mf(x)+m-1=0恰好有4个不相等的实数根,则实数m的取值范围是________.12.已知定义在R上的函数f(x)为增函数,且对任意x∈(0,+∞),有f[f(x)-log2x]=1恒成立,则函数f(x)的零点为________.13.已知函数g(x)=若函数f(x)=2x·g(lnx)+1-x2,则函数f(x)的零点个数为________.14.已知函数f(x)=2x,x∈R.(1)当m取何值时,方程|f(x)-2|=m分别有一个解、两个解?(2)若不等式f2(x)+f(x)-m>0在R上恒成立,求m的取值范围.15.运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油升,司机的工资是每小时14元.(1)求这次行车总费用y关于x的表达式;(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.16.如图61所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径r=mm,滴管内液体忽略不计.(1)如果瓶内的药液恰好156min滴完,问每分钟滴下多少滴?(2)在条件(1)下,设开始输液xmin后,瓶内液面与进气管的距离为hcm,已知当x=0时,h=13,试将h表示为x的函数.(注:1cm3=1000mm3)图61专题限时集训(六)【基础演练】1.A[解析]若m<0,则方程m+log2x=0(x≥1)有一解,即函数f(x)存在零点;反之,若函数f(x)有零点,则m≤0.所以“m<0”是“函数f(x)=m+log2x(x≥1)存在零点”的充分不必要条件.2.A[解析]易知f(x)在定义域内单调递增,且f=2-2<0,f=2-1>0,故选A.3.B[解析]画出函数y=tanx,y=在区间上的图像(图略),由图可知,两个函数的图像只有一个公共点,故函数f(x)=tanx-在区间内零点的个数为1.4.C[解析]由f(x+1)=f(x-1)得:函数f(x)是以2为周期的函数,由f(x)=f(-x+2)得:函数f(x)的图像关于直线x=1对称.又方程f(x)=0在[0,1]内有且只有一个根x=,因此在[1,2]内有且只有一个根x=,由周期性知f(x)=0在区间[0,2013]内有2013个根.5.-[解析]因为函数f(x)=ax+b的零点为x=2,所以2a+b=0,即=-2.由bx2-ax=0,得x=0或x==-.【提升训练】6.C[解析]画出函数y=f(x)和y=-x+m的图像,如图所示,则所求问题等价于两个函数的图像有交点,由图易知m∉(0,1],故m∈(-∞,0]∪(1,+∞).7.C[解析] 函数f(x)是定义域为R的奇函数,∴f(0)=0,又当x≤0时,f(x)=2x-x+a,∴20+a=0,解得a=-1,故当x≤0时,f(x)=2x-x-1.令f(x)=2x-x-1=0,解得x=-1或x=0,故f(-1)=0,则f(1)...