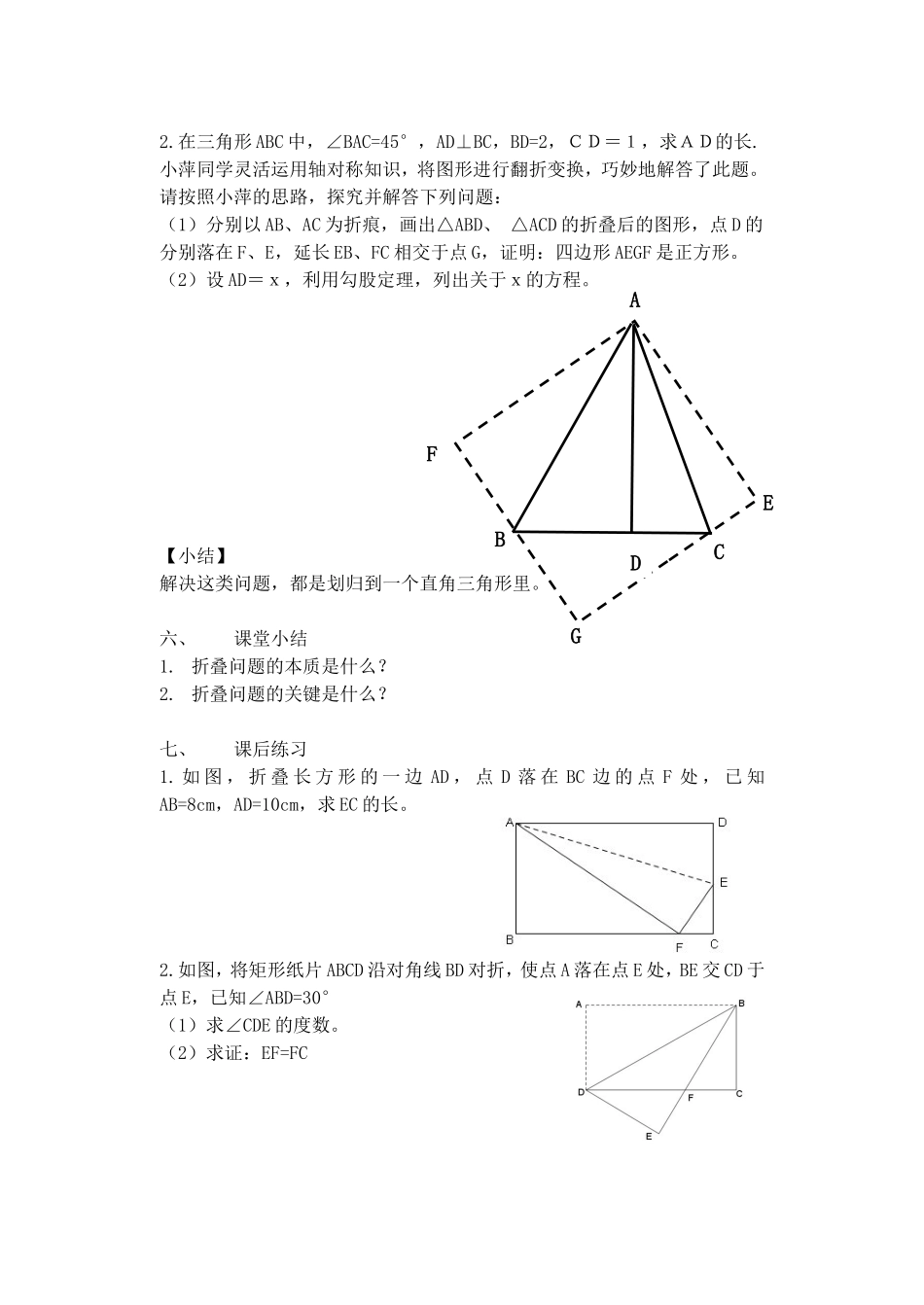
四边形的折叠问题丹阳市里庄初级中学甘浏一、引入小游戏:折纸飞机二、情境创设问题1:刚才叠小飞机运用了什么知识点?问题2:对称的两个图会怎样?问题3:折痕所在直线是什么?问题4:对称两点的连线与折痕有什么关系?透过现象看本质:透过折叠的现象,发现其本质就为_______,关键是___________三、合作探究将一张平行四边形纸片折一次,使折痕平分这个平行四边形的面积,这样的折叠方法有几种?这些折痕有什么共性?四、动手操作问题5:将平行四边形纸片沿着∠BAD的角平分线AE折叠,你能找到点B的对应点B′吗?问题6:此时构成的四边形ABEB′是什么四边形?问题7:平行四边形ABCD,AC⊥AB,若将平行四边形沿AC进行折叠,你能找到点B的对应点B′吗?问题8:这时构成的四边形ACDE′是什么四边形?问题9:给平行四边形ABCD添一个什么条件,矩形ACDE′就能成为正方形?五、实战演练1.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,(1)BE与BF相等吗?(2)你会求BE的长吗?(3)你会求⊿BEF的面积吗?ABCDABCD2.在三角形ABC中,∠BAC=45°,AD⊥BC,BD=2,CD=1,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题。请按照小萍的思路,探究并解答下列问题:(1)分别以AB、AC为折痕,画出△ABD、△ACD的折叠后的图形,点D的分别落在F、E,延长EB、FC相交于点G,证明:四边形AEGF是正方形。(2)设AD=x,利用勾股定理,列出关于x的方程。【小结】解决这类问题,都是划归到一个直角三角形里。六、课堂小结1.折叠问题的本质是什么?2.折叠问题的关键是什么?七、课后练习1.如图,折叠长方形的一边AD,点D落在BC边的点F处,已知AB=8cm,AD=10cm,求EC的长。2.如图,将矩形纸片ABCD沿对角线BD对折,使点A落在点E处,BE交CD于点E,已知∠ABD=30°(1)求∠CDE的度数。(2)求证:EF=FCGAFECBD