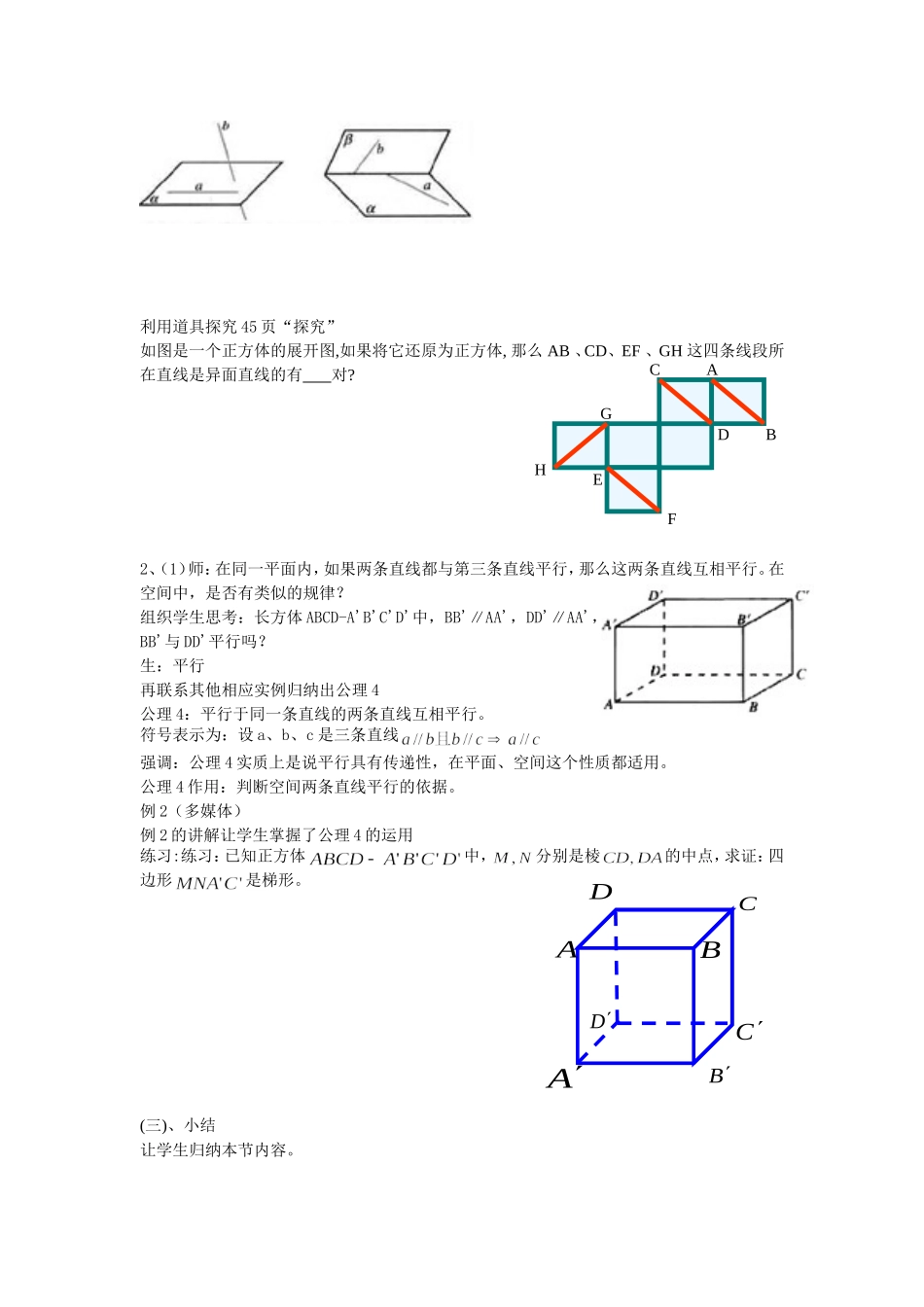
空间中直线与直线之间的位置关系(教案)一、三维目标:1、知识与技能(1)、了解空间两直线的三种位置关系,理解异面直线的定义。(2)、掌握平行公理、并能简单应用。2、过程与方法3、通过实例发现空间两条直线的三种位置关系,学会用自然语言、图形语言、符号语言加以描述,在此基础上,学习平行公理。通过对空间两条直线的学习,培养学生的画图能力和空间想象能力;通过运用公理4及定理解决简单问题,进一步培养将空间问题转化为平面问题的能力和逻辑思维能力;把问题教给学生,让学生自主解决,培养学生独立学习的习惯。二、教学重点、难点1、了解空间两条直线的位置关系,并学会用图形及符号表示。2、理解公里4,并能简单应用。复习回顾:1、同一平面内的两条直线有几种位置关系?空间中的两条直线呢?(板书课题)2,在长方体中,共有条棱,其中:(1)、与棱相交的有条棱,分别是;(2)、与棱平行的有条棱,分别是;(3)、剩余条棱,它们是。(二)讲授新课1、由问题2引出异面直线的定义,强调定义中“不同在任何一个平面”的含义。引导学生得出空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线:不同在任何一个平面内,没有公共点。补充习题练习:判断对错:1、空间中两条不相交的直线为异面直线()2、分别为有两个平面内的两条直线一定是异面直线()3、平面内的一条直线和平面外的一条直线一定是异面直线()教师再次强调异面直线不共面的特点,作图时通常用一个或两个平面衬托,如下图:共面直线利用道具探究45页“探究”如图是一个正方体的展开图,如果将它还原为正方体,那么AB、CD、EF、GH这四条线段所在直线是异面直线的有对?2、(1)师:在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相平行。在空间中,是否有类似的规律?组织学生思考:长方体ABCD-A'B'C'D'中,BB'∥AA',DD'∥AA',BB'与DD'平行吗?生:平行再联系其他相应实例归纳出公理4公理4:平行于同一条直线的两条直线互相平行。符号表示为:设a、b、c是三条直线强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。公理4作用:判断空间两条直线平行的依据。例2(多媒体)例2的讲解让学生掌握了公理4的运用练习:练习:已知正方体中,分别是棱的中点,求证:四边形是梯形。(三)、小结让学生归纳本节内容。FHCBEDGADACBABCD