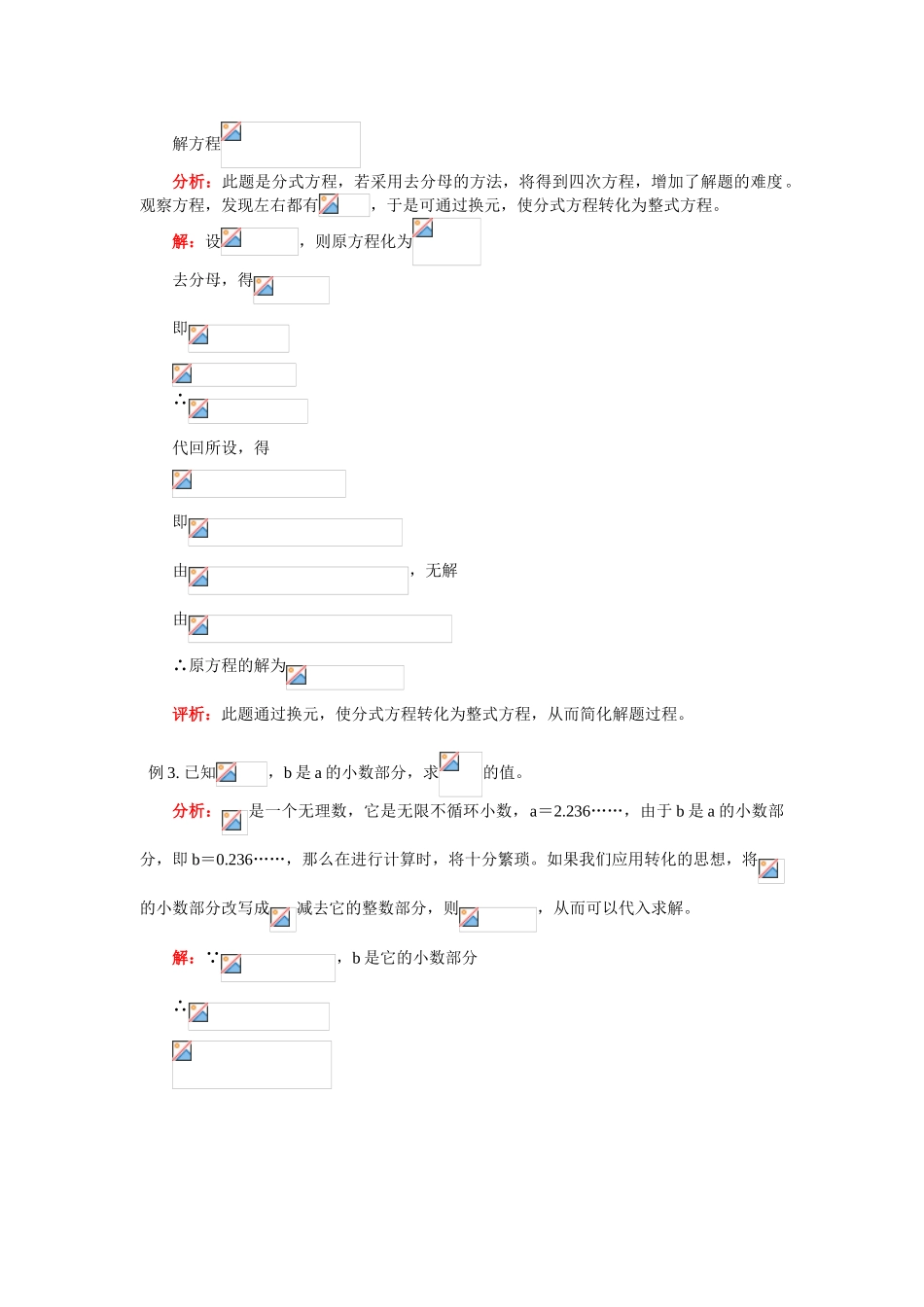
初三数学实际问题中转化思想的运用【本讲主要内容】实际问题中转化思想的运用包括解方程中转化思想的运用,以及解几何问题中转化思想的运用。【知识掌握】【知识点精析】1.解双二次方程中转化思想的运用;2.解分式方程中转化思想的运用;3.解无理方程中转化思想的运用;4.解几何问题中转化思想的运用。【解题方法指导】例1.解方程分析:此题是四次方程,我们通过换元可将它转化为一元二次方程去解,可设。解:设,则得∴∴即由解得由解得∴原方程的解为评析:解高次方程时,利用换元法转化为一元二次方程,从而使“不可解”转化为可解。例2.(2003年天津市)解方程分析:此题是分式方程,若采用去分母的方法,将得到四次方程,增加了解题的难度。观察方程,发现左右都有,于是可通过换元,使分式方程转化为整式方程。解:设,则原方程化为去分母,得即∴代回所设,得即由,无解由∴原方程的解为评析:此题通过换元,使分式方程转化为整式方程,从而简化解题过程。例3.已知,b是a的小数部分,求的值。分析:是一个无理数,它是无限不循环小数,a=2.236……,由于b是a的小数部分,即b=0.236……,那么在进行计算时,将十分繁琐。如果我们应用转化的思想,将的小数部分改写成减去它的整数部分,则,从而可以代入求解。解: ,b是它的小数部分∴评析:此题的转化思想运用得很巧妙,它是应用无理数=整数部分+小数部分,改写成小数部分=无理数-整数部分,从而化繁为简,化难为易。例4.已知:如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,平行四边形ABCD的周长为20,面积为18,。求sin∠EDF的值。分析:由平行四边形ABCD的周长为20,且,则它的四条边长都可求出,又由于知道平行四边形ABCD的面积,于是又可求出DE、DF的长,但欲求sin∠EDF的值,需构造出直角三角形,或在图中寻找到与∠EDF相等的角,不难发现∠A=∠EDF,于是将求sin∠EDF的值,转化为求sinA的值的问题加以解决。解: 平行四边形ABCD的周长为20,AB=∴AB+AD=10代入,得即∴AD=4,AB=6又AB·DE=18,∴DE=3在平行四边形ABCD中∠B+∠EDF=360°-2×90°=180°∠A+∠B=180°∴∠A=∠EDF∴评析:此题比较巧妙地将求sin∠EDF的值,转化为求sinA的值,从而应用锐角三角函数的定义加以解决,这种通过相等角的转化应用很广泛,要学会应用。【考点突破】【考点指要】转化思想是一种十分重要的数学思想,通过这种转化可以将高次方程转化为低次方程,将分式方程转化为整式方程,将无理方程转化为有理方程,从而将生疏的问题转化为熟练的问题,将复杂的问题转化为简单的问题。在解决几何问题时,又常利用相等线段的转化或相等角的转化,使问题由看来“不可解”转化为“可解”。正因为转化思想的应用广泛性,因此在中考试题中各省市都加大了考试的力度,命题的频率非常高,应引起广大同学的重视。【典型例题分析】例1.(2001年河南)解方程:分析:此题是一个无理方程,若采用方程两边同时平方的方法,将会出现四次方程,观察题目特点,发现根号内有,根号外有,于是可将先化为,再通过换元,转化为有理方程去解。解:原方程变形为设,则则原方程化为解得当y=3时,∴得解得当y=-1时,方程无解经检验,是原方程的解评析:此题通过换元,将无理方程转化为有理方程,从而使方程易解。此题解题方法不唯一。例2.已知求的值。分析:若解关于a的方程,关于b的方程,然后代入求值,由于出现无理根,解法将会很繁琐。认真分析所给的两个方程,发现a、b是方程的两个根,由一元二次方程根与系数的关系,得出,再代入求值便会变得十分简单。解: ∴a、b是方程的两个根由一元二次方程根与系数关系,得∴评析:此题解法很巧妙,是由转化为a、b是方程的两个根,从而用一元二次方程根与系数关系求解,这种转化的方法很特殊,可以仔细加以体会。例3.已知:如图,AB是⊙O直径,BC切⊙O于B,AC交⊙O于D,E是弧AD上一点,且∠EAD=∠CAB,又。求DE的长。分析:由于DE是⊙O的一条弦,它又是斜三角形的一条边,求它的长度存在一定的困难。由条件中∠EAD=∠CAB,可知弧DE=弧DB,于是可得DE=DB,这样,求DE的长的问题便转化为求DB...