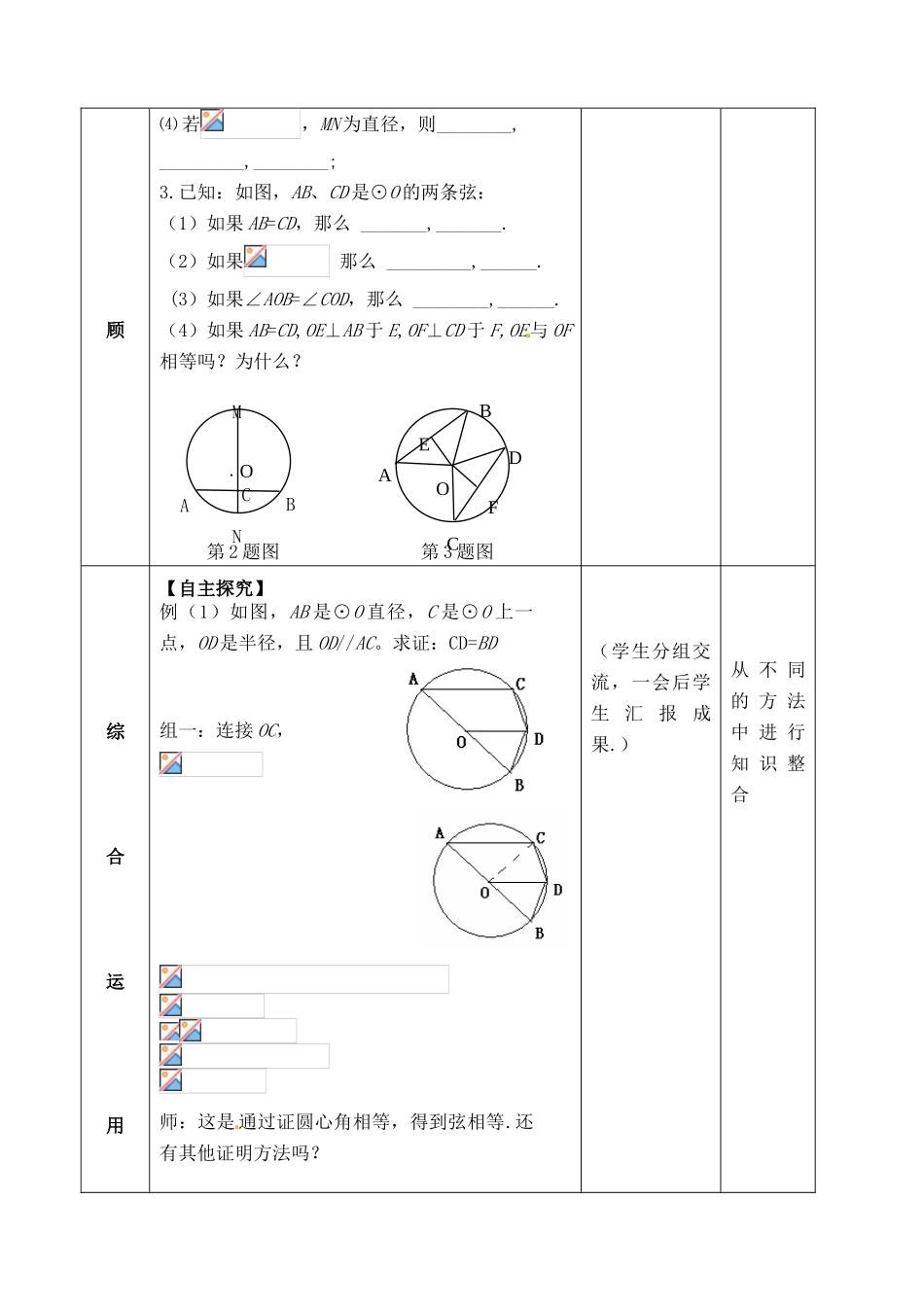
圆的有关性质一、【教材分析】教学目标知识技能1.知道圆、弧、弦、圆心角、圆周角等基本概念;认识圆的对称性.2.能用垂径定理,圆心角、弧、弦之间关系定理,圆周角定理及推论等进行简单的运算和推理;会通过作图的方法理解确定圆的条件.3.会用折叠、旋转、圆的对称性及分类讨论的思想方法探索图形的有关性质,能将有关弦长、半径的实际计算问题转化成解直角三角形问题解决.过程方法通过知识点和典型题的练习,熟练掌握本节课的知识点,再用题图变形与题组训练来培养综合运用知识的能力以及思维的灵活性和广阔性.情感态度在解决问题的过程中,养成认真、独立思考、合作交流等学习习惯.教学重点关于圆的有关计算和证明.教学难点将圆的有关性质运用到计算和逻辑推理中.二、【教学流程】教学环节教学问题设计师生活动二次备课知识回【回顾练习】1.________________上的三点确定________个圆。2.如图:在⊙O中,⑴若MN⊥AB,MN为直径则________,_________,________;⑵若AC=BC,MN为直径,AB不是直径,则________,_________,________;⑶若MN⊥AB,AC=BC则______,_______,______;通过回顾练习,生总结归纳所用知识点、方法及规律,然后组内交流,补充完善对问题的认识和方法.顾⑷若,MN为直径,则________,_________,________;3.已知:如图,AB、CD是⊙O的两条弦:(1)如果AB=CD,那么_______,_______.(2)如果那么_________,______.(3)如果∠AOB=∠COD,那么________,______.(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?第2题图第3题图综合运用【自主探究】例(1)如图,AB是⊙O直径,C是⊙O上一点,OD是半径,且OD//AC。求证:CD=BD组一:连接OC,师:这是通过证圆心角相等,得到弦相等.还有其他证明方法吗?(学生分组交流,一会后学生汇报成果.)从不同的方法中进行知识整合ADCBOEFMNBAC·O组二:连接AD,,OA=OD弧CD=弧BDCD=BD师:由圆周角相等,我们可以得到弧相等(或圆心角相等),从而得到弦相等.这种证法利用了圆心角、圆周角与弧的关系.在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于所对圆心角的一半;相等的圆周角所对的弧相等.这样,证弦相等,又多了两条途径:可以考虑去证弧相等,也可以考虑去证圆周角相等.师:还有其他方法吗?组三:连接BC,AB是直径AC//OD由垂径定理可以得到弧CD=弧BDCD=BD师:这就利用了垂径定理的基本图形.(边总结,边在黑板上抽离基本图形)(同时在黑板上画出这个基本图形)(同时在黑板上抽离这个基本图形.)从不同的方法中进行知识整合垂径定理及逆定理体现了直径、弧、弦三种量之间的关系:直径垂直弦、直径平分弦、直径平分弧,这三个结论中,只要有一个成立,则另两个也同时成立.但要注意,若条件是直径平分弦,则这条弦必须不是直径,另两个结论才会成立.垂径定理及逆定理体现的是圆的轴对称性.而在圆中,要构造直角,大家要想到直径所对的圆周角是直角;而的圆周角所对的弦是直径。连直径,作直角是圆中常添的辅助线方法。在圆中构造直角,还常作弦心距,弦心距、弦的一半、半径构成一个直角三角形,这在计算题中用得较多.师:还有其他方法吗?组四:延长DO交⊙O于点E,连接AE.弧AE=弧CDAE=CDCD=BD师:这也是圆中的一种基本图形,由弦平行,可以得到所夹弧相等。这个结论我们书上证明过,可以证一对内错角又是圆周角相等得到.若不添加任何辅助线,你能证明出来吗?(提示:已知的相等两角、的度数分别与弧的度数有什么关系?)从不同的方法中进行知识整合从不同的方法中进行知识整合组五:=弧BC的度数弧BD的度数弧BC=弧BD=弧CDCD=BD师:圆周角度数等于所对弧度数的一半,圆心角度数等于所对弧的度数.(2):延长AC、BD交于点E,连接BC,请判断:下面结论中正确的是______________.①AB=AE②BD=DE③∠E=2∠EBC④⑤△ECD∽△EBA(3)过点D做DG⊥AE,垂足为G,则四边形DGCF为什么四边形?为什么?(4)移动点D位置,使点D在弧AB中点处,令点C在弧AD之间,过D做DF⊥BC,DG⊥AE,垂足为E、F,则四边形DGCF是什么四边形?为什么?师:首先这个四边形已经是一个什么四边形?——矩形.那再证一个什么条件,矩形就能成为...