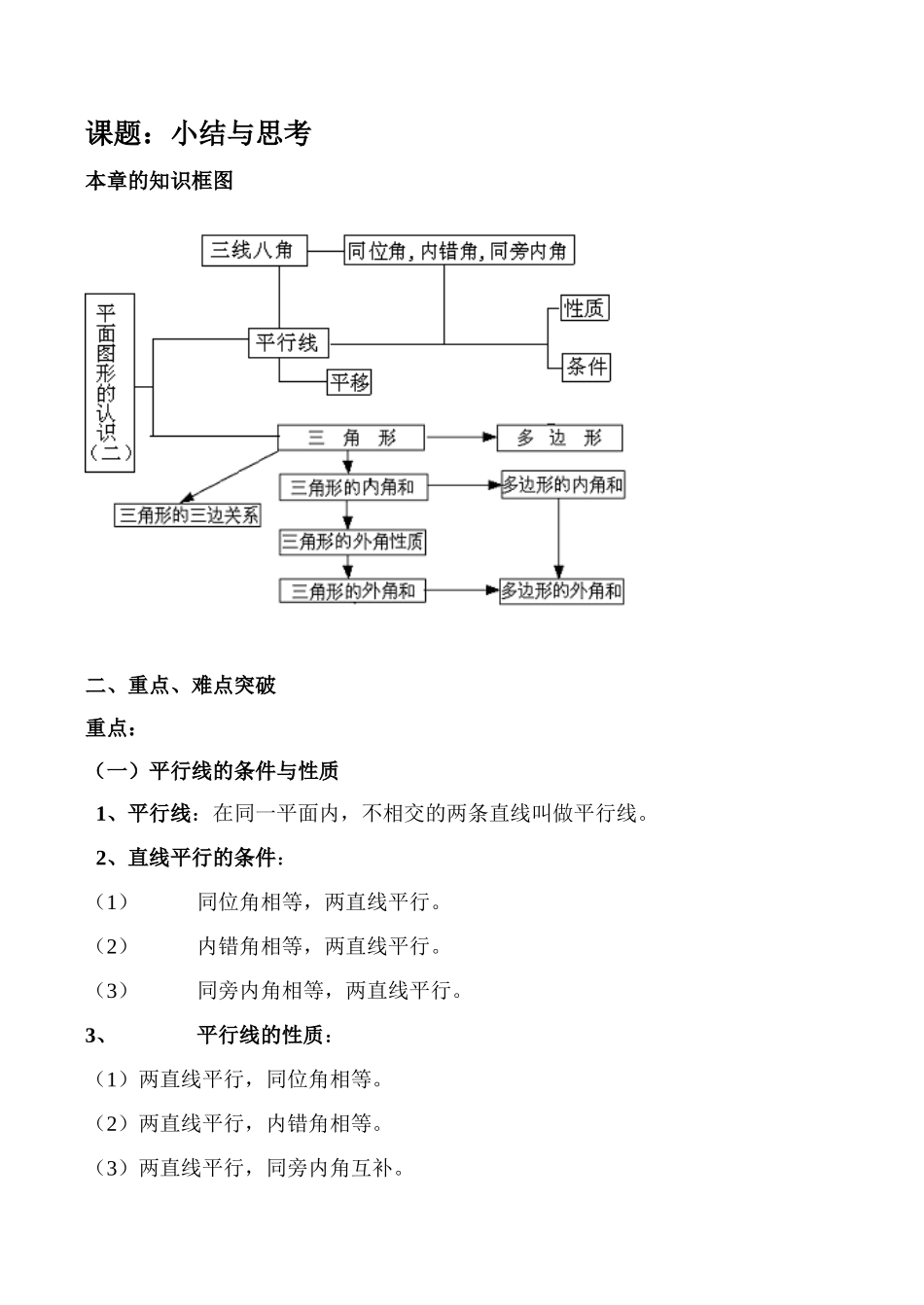
课题:小结与思考本章的知识框图二、重点、难点突破重点:(一)平行线的条件与性质1、平行线:在同一平面内,不相交的两条直线叫做平行线。2、直线平行的条件:(1)同位角相等,两直线平行。(2)内错角相等,两直线平行。(3)同旁内角相等,两直线平行。3、平行线的性质:(1)两直线平行,同位角相等。(2)两直线平行,内错角相等。(3)两直线平行,同旁内角互补。(二)平移1、平移的现象在日常生活中,我们经常看到滑雪运动员在平坦雪地上滑翔、大楼的电梯上上下下地运送来客、火车在笔直的铁路上飞驰、铝合金窗叶左右移动、升降机上下运东西、这些现象都是平移现象.2、平移的概念在一个平面内,将一个基本的图形沿一定的方向移动了一定的距离,这种图形平行移动称为平移.3、平移的特征由平移后的图形与原图形比较,可得出,平移后的图形与原图形的对应线段平行且相等,对应角相等,图形的形状与大小都没有发生变化,在平移过程中,对应线段有时平行,有时还可能在同一直线上,对应点所连的线段平行且相等,有时对应点的连线也可能会在同一直线上.4平移作图(1)已知原图和一对应点作出平移后的图形.(2)已知原图和一对应角作出平移后的图形.(3)已知原图平移距离作出平移后的图形.(三)三角形1、三边关系三角形中任意两边之和大于第三边是由“两点之间的所有线段中,线段最短”这个结论得到的,要注意知识之间的前后联系。2、按角分类在按角对三角形分类时,要明确分类的标准,注意分类时要做到“不重不漏”,同时注意到三角形三条边、三个角之间的关系与三角形的具体形状无本质关系,特殊三角形的特殊性质与其具体形状有关,如“直角三角形的两个锐角互余”。3、三线三角形中的高、角平分线、中线是三角形的几条重要线段。三角形中的三条高、三条角平分线、三条中线必交于一点,其中角平分线和中线的交点都在三角形内,而三条高的交点则要分类讨论。三角形的高线的画法实质的对直线外一点作已知直线的垂线,这是画出高线的关键,也是高线的本质,从易到难是分散难点和突破难点的具体措施和方法。4、三角形内角和理解三角形内角和为180°时,要结合学习过的有关平行线特征和识别的知识。5、多边形多边形(n边形):由n条不在同一直线上的线段首尾顺次连接组成的平面图形。凸多边形:如果沿着多边形任何一条边作直线,多边形均在直线的同侧。凹多边型:多边形存在若干这样的边,如果沿着这条边作直线,多边形在直线的两侧。正多边形:多边形的各边都相等且各角都相等。对角线:连接多边形不相邻的两个顶点的线段。n边形的内角和=(n-2)·180°任意多边形的外角和都为360°(外角和是指:每个顶点取且只取一个外角)。注意:(1)多边形的内角和仅与边数有关,与多边形的大小、形状无关;(2)凸多边形的内角α的范围:0°<α<180°6、任意多边形的内角和为(n-2)·180°(这里n表示边数),外角和是360°,需指出的是多边形内角和随边数的变化而变化,而外角和是一个定值,它不随边数的变化而变化,此类题目类型大致可分为:(1)已知边数,求内角和。其方法是直接将边数代入公式即可。(2)已知角度求边数。若已知内角和,则直接用内角和公式列方程可求边数;若已知一个内角的度数,则列出这个角度乘以n等于(n-2)·180°的方程,求边数;若已知一个外角的度数,则只需用外角和除以已知角的度数,即求出边数;若已知内、外角和的度数之比,则利用等于已知比,可求边数。难点:1、找同位角、内错角、同旁内角。2、能够运用平移的基础知识分析复杂图的形成过程。3、理解平移的性质.4、三边关系的理解,5、多边形内角和的运用整合拓展创新类型之一、平行线的条件和性质例1如图7-1,已知∠BED=∠B+∠D,则AB//CD,为什么?7-1【思路分析】要得到AB//CD,从已知条件看,只有作EF//AB或EF//CD,借助于已知条件,得出内错角相等,然后才有EF//CD或EF//AB。解:过E作EF//AB,则∠BED=∠BEF+∠FED因为EF//AB所以∠BEF=∠B于是∠BED=∠B+∠FED又∠BED=∠B+∠D所以∠FED=∠D所以EF//CD。而EF//AB所以AB//CD。【点评】本题主要是“两直线平行,内错角相等”的正、逆向...