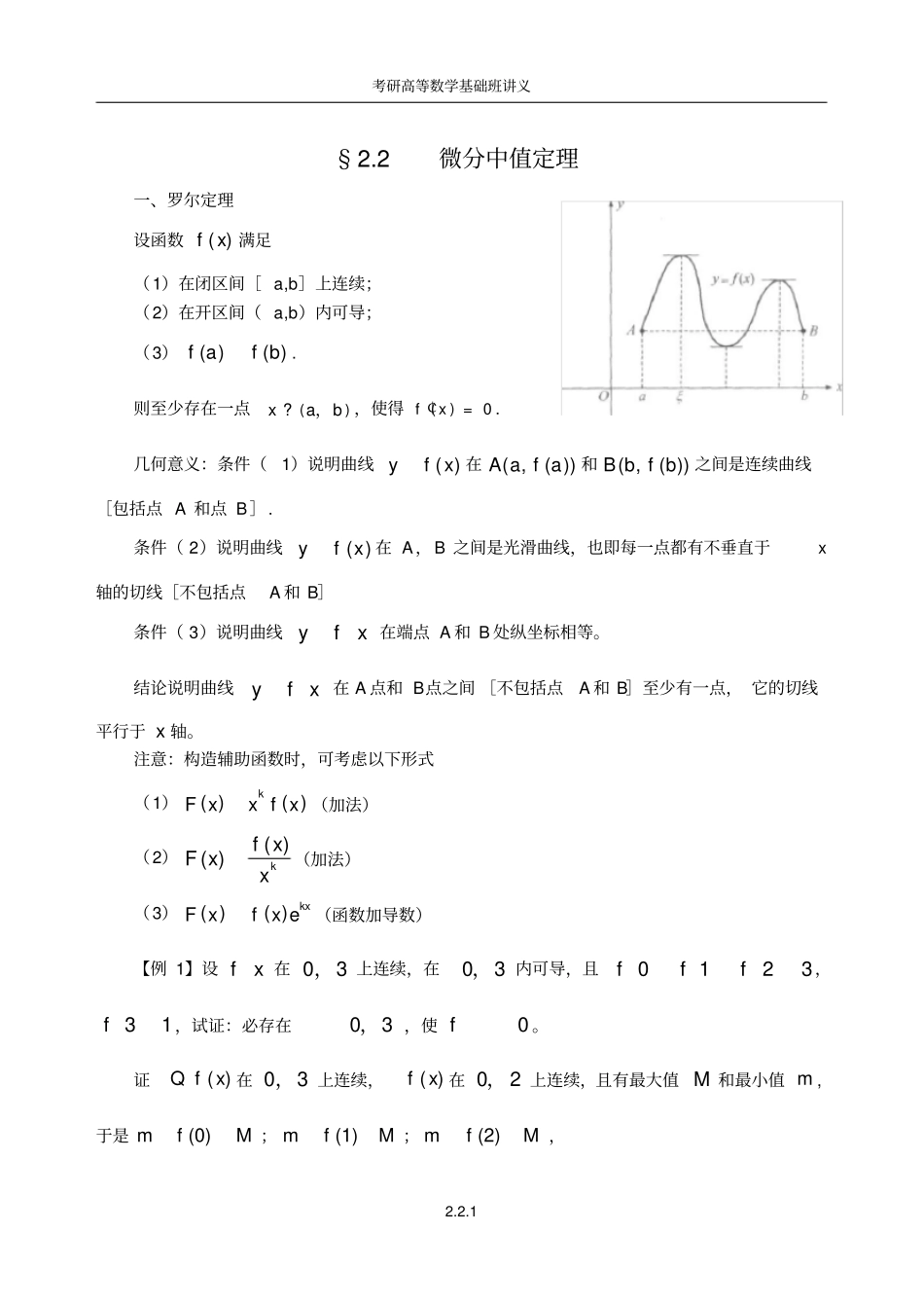
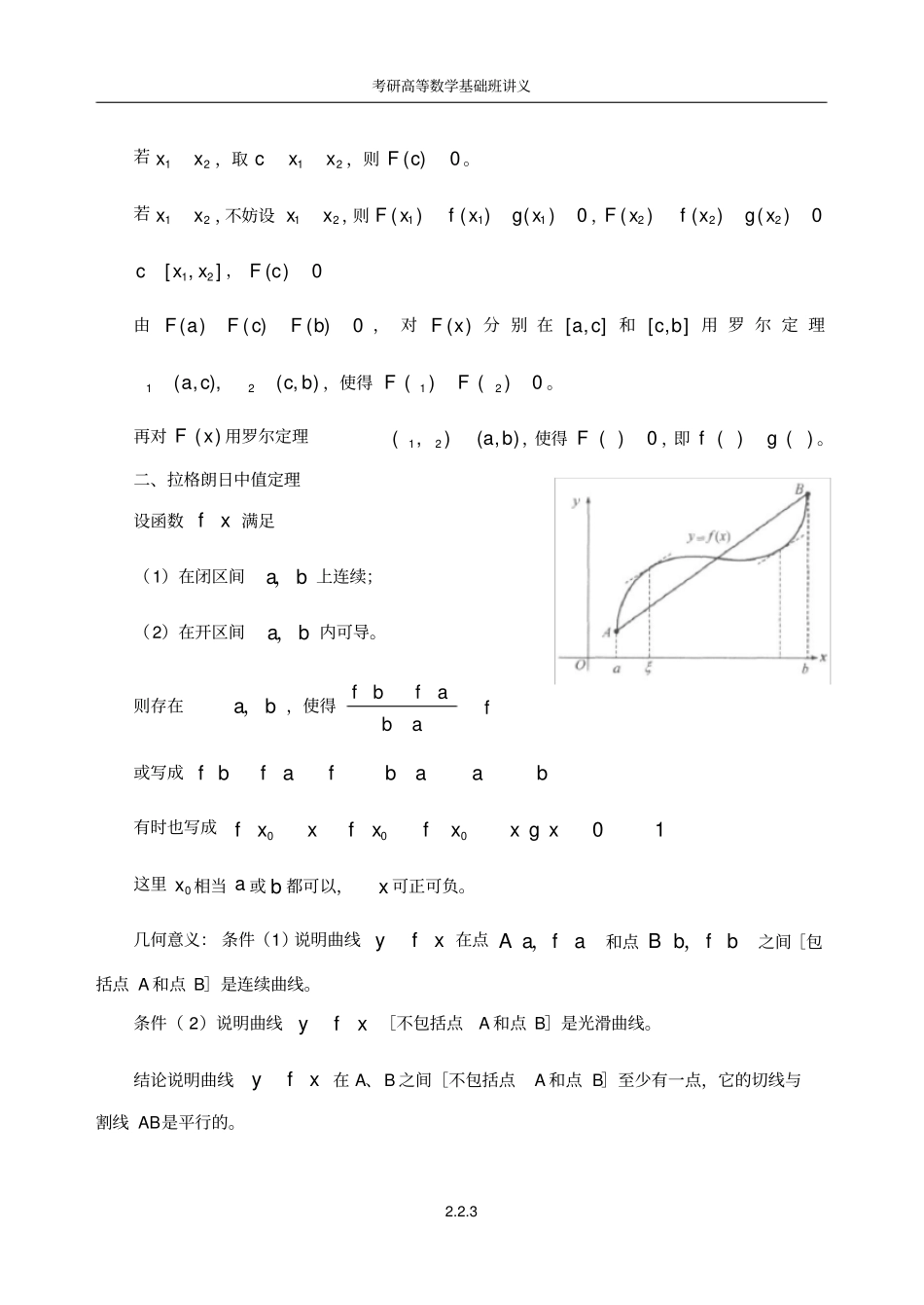
考研高等数学基础班讲义2.2.1§2.2微分中值定理一、罗尔定理设函数()fx满足(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)()()fafb.则至少存在一点()abx?,,使得()0fx¢=.几何意义:条件(1)说明曲线()yfx在(,())Aafa和(,())Bbfb之间是连续曲线[包括点A和点B].条件(2)说明曲线()yfx在A,B之间是光滑曲线,也即每一点都有不垂直于x轴的切线[不包括点A和B]条件(3)说明曲线yfx在端点A和B处纵坐标相等。结论说明曲线yfx在A点和B点之间[不包括点A和B]至少有一点,它的切线平行于x轴。注意:构造辅助函数时,可考虑以下形式(1)()()kFxxfx(加法)(2)()()kfxFxx(加法)(3)()()kxFxfxe(函数加导数)【例1】设fx在0,3上连续,在0,3内可导,且0123fff,31f,试证:必存在0,3,使0f。证()fxQ在0,3上连续,()fx在0,2上连续,且有最大值M和最小值m,于是(0)mfM;(1)mfM;(2)mfM,考研高等数学基础班讲义2.2.2故1(0)(1)(2)3mfffM。由连续函数介值定理可知,至少存在一点c0,2,使得1(0)(1)(2)13fcfff因此3fcf,且fx在c,3上连续,c,3内可导,由罗尔定理得出必存在03c,3,,使得0f。【例2】设fx在0,1上连续,在01,内可导,且23130fxdxf.求证:存在()0,1x?使()0fx¢=证由积分中值定理可知,存在轾?犏臌2,13c,使得231213fxdxfc得到2313(0)fcfxdxf对fx在0c,上用罗尔定理(三个条件都满足),故存在()0(01)c,,x翁,使()0fx¢=【例3】(07)设函数()fx,()gx在[,]ab上连续,在(,)ab内具有二阶导数且存在相等的最大值,()(),()()fagafbgb,证明:存在(,)ab,使得()()fg。分析:令()()()()FxfxgxFx在[,]ab连续,在(,)ab可导,在题设条件下,要证存在(,)ab,()0F。已知()()0FaFb,只需由题设再证(,)cab,()0Fc。证明:由题设11[,](,),max()()abxabMfxfx,22[,](,),max()()abxabMgxgx。考研高等数学基础班讲义2.2.3若12xx,取12cxx,则()0Fc。若12xx,不妨设12xx,则111()()()0Fxfxgx,222()()()0Fxfxgx12[,]cxx,()0Fc由()()()0FaFcFb,对()Fx分别在[,]ac和[,]cb用罗尔定理12(,),(,)accb,使得12()()0FF。再对()Fx用罗尔定理12(,)(,)ab,使得()0F,即()()fg。二、拉格朗日中值定理设函数fx满足(1)在闭区间ab,上连续;(2)在开区间ab,内可导。则存在ab,,使得fbfafba或写成fbfafbaab有时也写成00001fxxfxfxxxg这里0x相当a或b都可以,x可正可负。几何意义:条件(1)说明曲线yfx在点Aafa,和点Bfbb,之间[包括点A和点B]是连续曲线。条件(2)说明曲线yfx[不包括点A和点B]是光滑曲线。结论说明曲线yfx在A、B之间[不包括点A和点B]至少有一点,它的切线与割线AB是平行的。考研高等数学基础班讲义2.2.4推论1若fx在ab,内可导,且0fx,则fx在ab,内为常数。推论2若fxgx,在ab,内皆可导,且fxgx,则在ab,内fxgxc,其中c为一个常数。推论3设()fx,()gx在[,]ab上连续,在(,)ab内可导,则000(1)()(),(,)()()([,])(2)[,],()()fxgxxabfxgxxabxabfxgx(注:拉格朗日中值定理为罗尔定理的推广,当fafb时的特殊情形,就是罗尔定理)【例1】设不恒为常数的函数fx在ab,上连续,ab,内可导,且fafb,证明ab,内至少有一点ξ,使得0f.证由题意可知存在(,)cab?使得fcfafb如果fcfa,则fx在ac,上用拉格朗日中值定理存在1(,)acx?,使1()()0fcfafca如果fbfc,则fx在cb,上用拉格朗日中值定理存在2(,)cbx?,使2()()0fbfcfbc,因此,必有(,)abx?,使得0f成立.【例2】设()0fx,(0)0f=,证明对任意10x>,20x>恒有1212()()()fxxfxfx+<+证不妨假设12xx£,由拉格朗日中值定理有考研高等数学基础班讲义2.2.5①1111()()(0)(0)()fxfxfxfx¢=-=-,110xx<<②[]1221222()()()()fxxfxxxxfx¢+-=+-,2212xxxx<<+,从而可知12xx<, ()0fxⅱ<, ()fx¢单调减少,于是12()()ffxxⅱ>这样由①②两式可知1122()()()fxfxxfx>+-因此,1212()()()fxxfxfx+<+成立.【例3】(04)设2eabe,证明2224lnln()babae.分析:即证222lnln4()babae,符合拉格朗日中值定理。证明:令2()lnfxx,在[,]ab上用拉格朗日中值定理得22()()lnlnln()2fbfabafbaba,其中2(,)(,)abee。注意到ln()xxx,则21ln()0()...