1.5.1二项式定理1

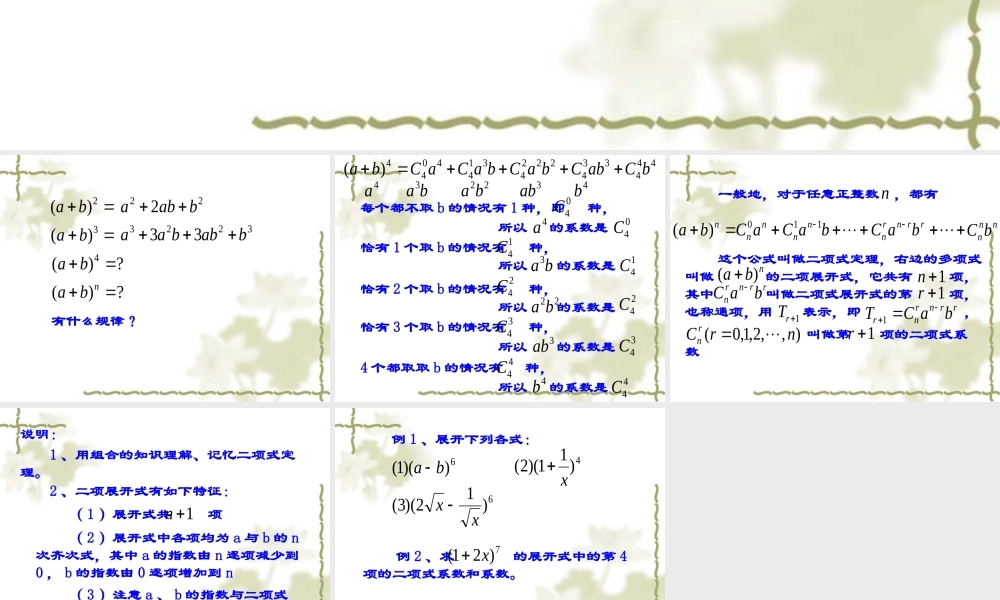
1.5.1 二项式定理（一）有什么规律？2)(ba222baba3)(ba322333babbaa?)(4 ba?)(nba22ba4a4b3abba34)(ba每个都不取 b 的情况有 1 种，即 种，04C所以 的系数是4a04C恰有 1 个取 b 的情况有 种，14C所以 的系数是14Cba3恰有 2 个取 b 的情况有 种，24C恰有 3 个取 b 的情况有 种，34C所以 的系数是22ba24C所以 的系数是3ab34C4 个都取取 b 的情况有 种，44C所以 的系数是4b44C4443342224314404bCabCbaCbaCaC 一般地，对于任意正整数 ，都有nnba)(nnaC0baCnn11rrnrnbaCnnnbC 这个公式叫做二项式定理，右边的多项式叫做 的二项展开式，它共有 项，其中 叫做二项式展开式的第 项，也称通项，用 表示，即 ， nba)( 1nrrnrnbaC1r1rTrrnrnrbaCT 1 叫做第 项的二项式系数1r),,2,1,0(nrCrn说明： 1 、用组合的知识理解、记忆二项式定理。 2 、二项展开式有如下特征： （ 2 ）展开式中各项均为 a 与 b 的 n次齐次式，其中 a 的指数由 n 逐项减少到0 ， b 的指数由 0 逐项增加到 n （ 3 ）注意 a 、 b 的指数与二项式系数的对应关系。 3 、注意二项式系数与系数的区别。 （ 1 ）展开式共 项1n例 1 、展开下列各式：6))(1(ba 4)11)(2(x6)12)(3(xx  例 2 、求 的展开式中的第 4项的二项式系数和系数。7)21(x