1.5.1二项式定理(2)

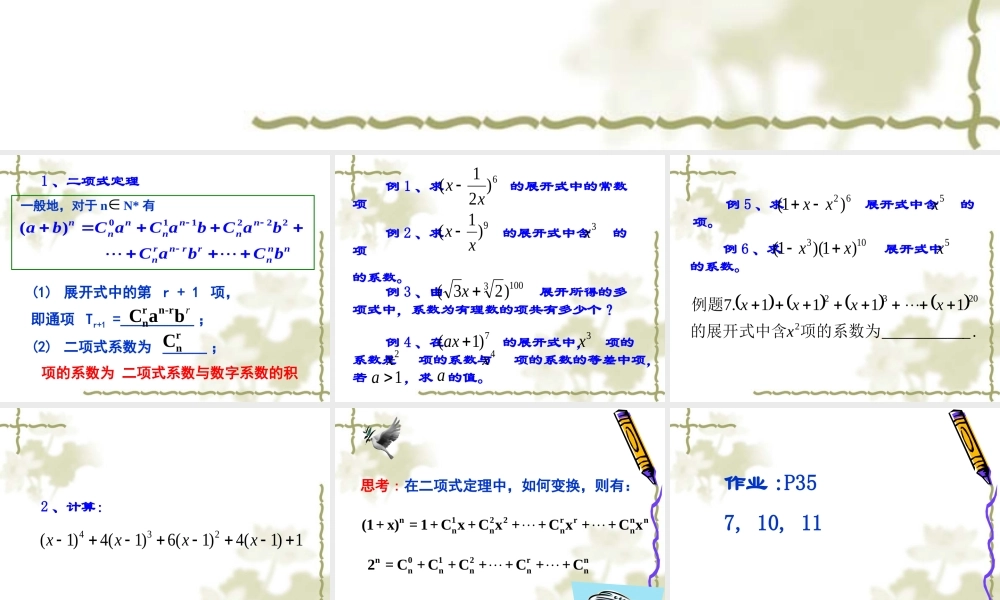
1.5.1 二项式定理（二） 1 、二项式定理一般地，对于 n N* 有011222()nnnnnnnrn rrnnnnabC aC abC abC abC b(1) 展开式中的第 r + 1 项，即通项 Tr+1 =__________ ；rrn-rnC ab(2) 二项式系数为 ______ ；项的系数为 二项式系数与数字系数的积rnC 例 1 、求 的展开式中的常数项6)21(xx  例 2 、求 的展开式中含 的项的系数。9)1(xx 3x 例 3 、由 展开所得的多项式中，系数为有理数的项共有多少个？1003)23(x 例 4 、在 的展开式中， 项的系数是 项的系数与 项的系数的等差中项，若 ，求 的值。7)1(ax3x2x4x1aa 例 5 、求 展开式中含 的项。5x62)1(xx  例 6 、求 展开式中 的系数。103)1)(1(xx5x .___________1111.722032项的系数为的展开式中含例题xxxxx1)1(4)1(6)1(4)1(234xxxx2 、计算： 思考 : 在二项式定理中，如何变换，则有：n122rrnnnnnn(1+ x) = 1+C x +C x ++C x ++C xn012rnnnnnn2 = C +C +C ++C ++C 作业 :P357, 10, 11