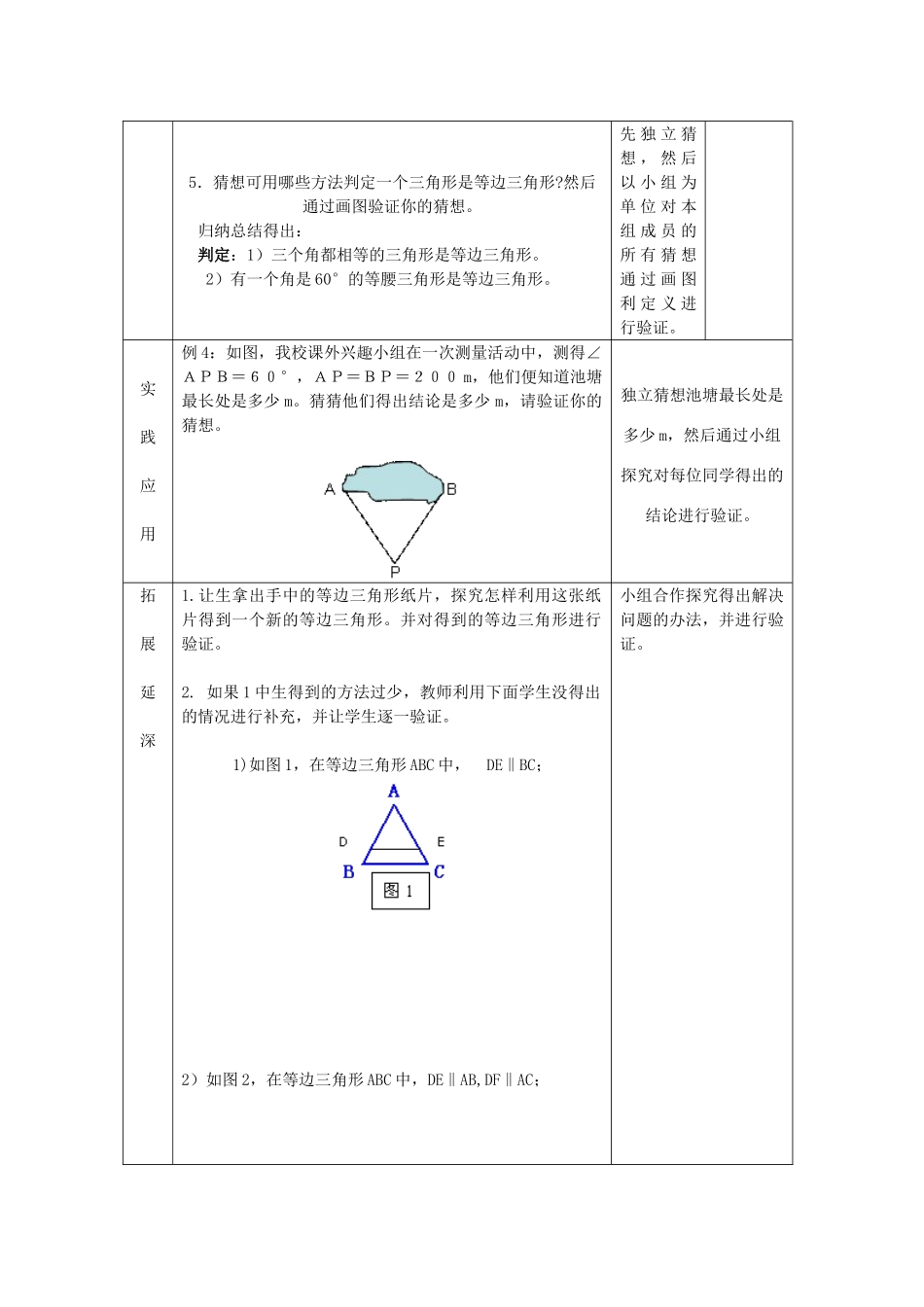
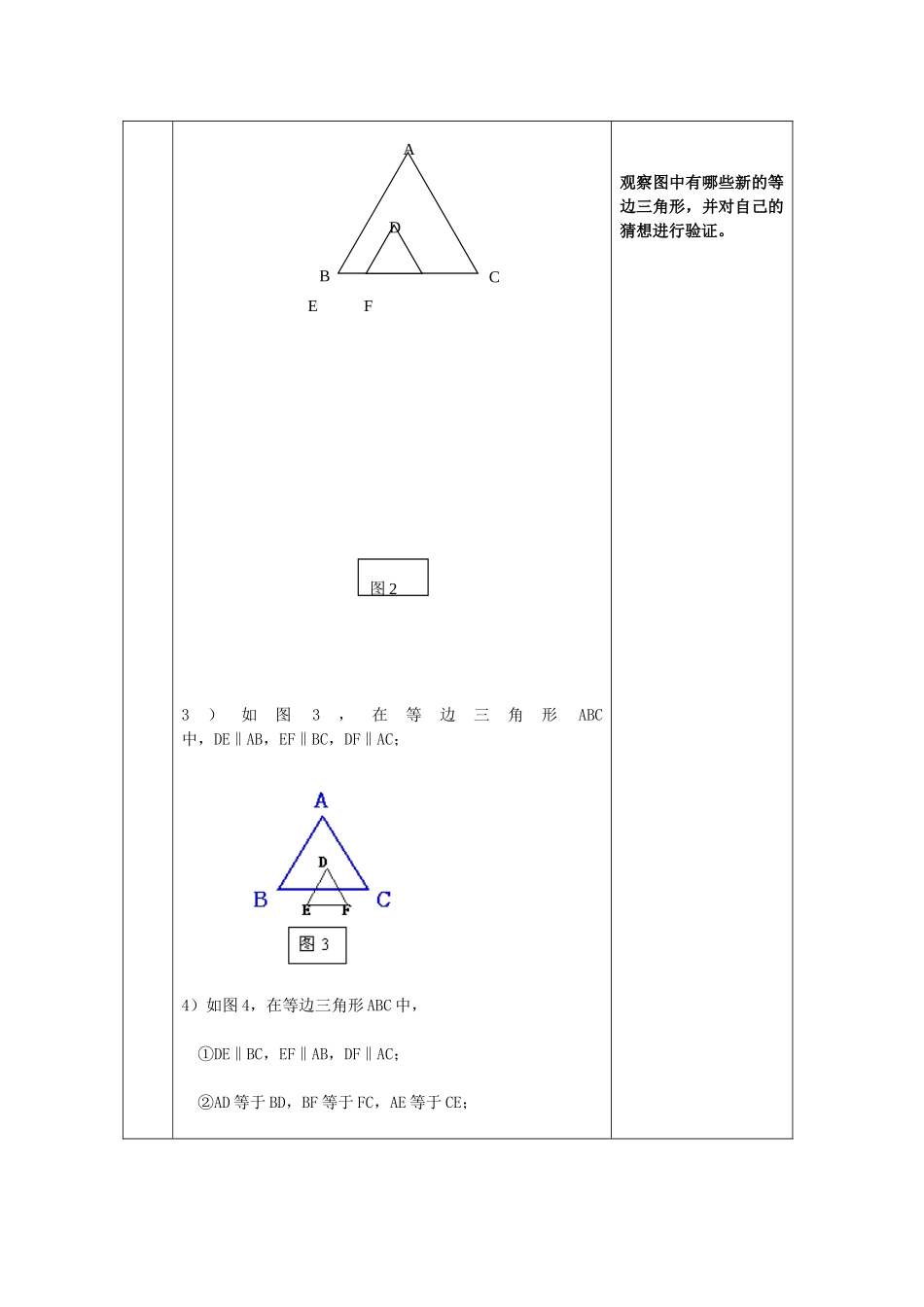
2、5等腰三角形的轴对称性3—等边三角形教学课题课型新授本课题时数:1本课时为第一教时教学重点:等边三角形的性质和判定形成与应用教学难点:等边三角形性质与判定的应用教学方法与手段:讲练结合教学过程教师活动学生活动设计意图创设问题情境1.出示等边三角形图片.2.提出问题:房子的顶部是什么图形?同学们想不想更深入的了解等边三角形的知识?从而导入新课。板书课题[等边三角形].观察图片,口答问题。探索新知1、提出问题:根据原来学习图形的经验你认为应从哪些方面研究等边三角形?思考后口答2、让学生从试着给等边三角形下定义。3、归纳小结得出:定义:三条边都相等的三角形叫做等边三角形。独立思考后表达交流,得出结论。4、观察课前准备的等边三角形纸片,猜想等边三角形有哪些性质,并通过测量、折纸、证明等方式进行验证。归纳总结得出:性质:等边三角形三个内角都相等,并且每一个角都等于60°。以小组为单位先猜想、再通过合作探究,得出结论后表达交流。要求要求学生用正确的书面语说出等边三角形的性质5.猜想可用哪些方法判定一个三角形是等边三角形?然后通过画图验证你的猜想。归纳总结得出:判定:1)三个角都相等的三角形是等边三角形。2)有一个角是60°的等腰三角形是等边三角形。先独立猜想,然后以小组为单位对本组成员的所有猜想通过画图利定义进行验证。实践应用例4:如图,我校课外兴趣小组在一次测量活动中,测得∠APB=60°,AP=BP=200m,他们便知道池塘最长处是多少m。猜猜他们得出结论是多少m,请验证你的猜想。独立猜想池塘最长处是多少m,然后通过小组探究对每位同学得出的结论进行验证。拓展延深1.让生拿出手中的等边三角形纸片,探究怎样利用这张纸片得到一个新的等边三角形。并对得到的等边三角形进行验证。2.如果1中生得到的方法过少,教师利用下面学生没得出的情况进行补充,并让学生逐一验证。1)如图1,在等边三角形ABC中,DE‖BC;2)如图2,在等边三角形ABC中,DE‖AB,DF‖AC;小组合作探究得出解决问题的办法,并进行验证。3)如图3,在等边三角形ABC中,DE‖AB,EF‖BC,DF‖AC;4)如图4,在等边三角形ABC中,①DE‖BC,EF‖AB,DF‖AC;②AD等于BD,BF等于FC,AE等于CE;观察图中有哪些新的等边三角形,并对自己的猜想进行验证。ACBD图2FE5)如图5,在等边三角形ABC中,AD=BE=CF。归纳小结通过本节课的学习你有什么收获?作业完成补充习题《1、5等腰三角形的轴对称性》习题教学反思本课内容从生活实际中,房子的图形引入等边三角形,激发起学生的学习兴趣,使下面的内容能在愉快的状态下进行,能更好掌握新知。灵活应用等边三角形的性质与判定解决相关的几何问题还需加强训练。学案课题:等边三角形班级姓名一、等边三角形的定义:三边相等的三角形叫做等边三角形或正三角形。二、等边三角形的性质:等边三角形是轴对称图形,并且有3条对称轴。等边三角形的每个角都等于600。如图在△ABC中,∵AB=BC=AC∴===。ACB思考:1、3个角相等的三角形是等边三角形吗?为什么?2、有两个角是600的三角形是等边三角形吗?为什么?例题:1、有一个角是600的等腰三角形是等边三角形吗?为什么?2、如图,我校课外兴趣小组在一次测量活动中,测得∠APB=60°,AP=BP=200m,他们便知道池塘最长处是多少m。猜猜他们得出结论是多少m,请验证你的猜想。拓展:1、请学生在纸上画一个等边三角形,然后按如下方法添加辅助线,看一看有没有新的正三角形产生?1)如图1,在等边三角形ABC中,DE‖BC;FEACBD2)如图2,在等边三角形ABC中,DE‖AB,DF‖AC;3)如图3,在等边三角形ABC中,DE‖AB,EF‖BC,DF‖AC;4)如图4,在等边三角形ABC中,①DE‖BC,EF‖AB,DF‖AC;②AD等于BD,BF等于FC,AE等于CE;5)如图5,在等边三角形ABC中,AD=BE=CF。巩固:课本P28练习1、2。作业:课本P29习题第10、12小题图2