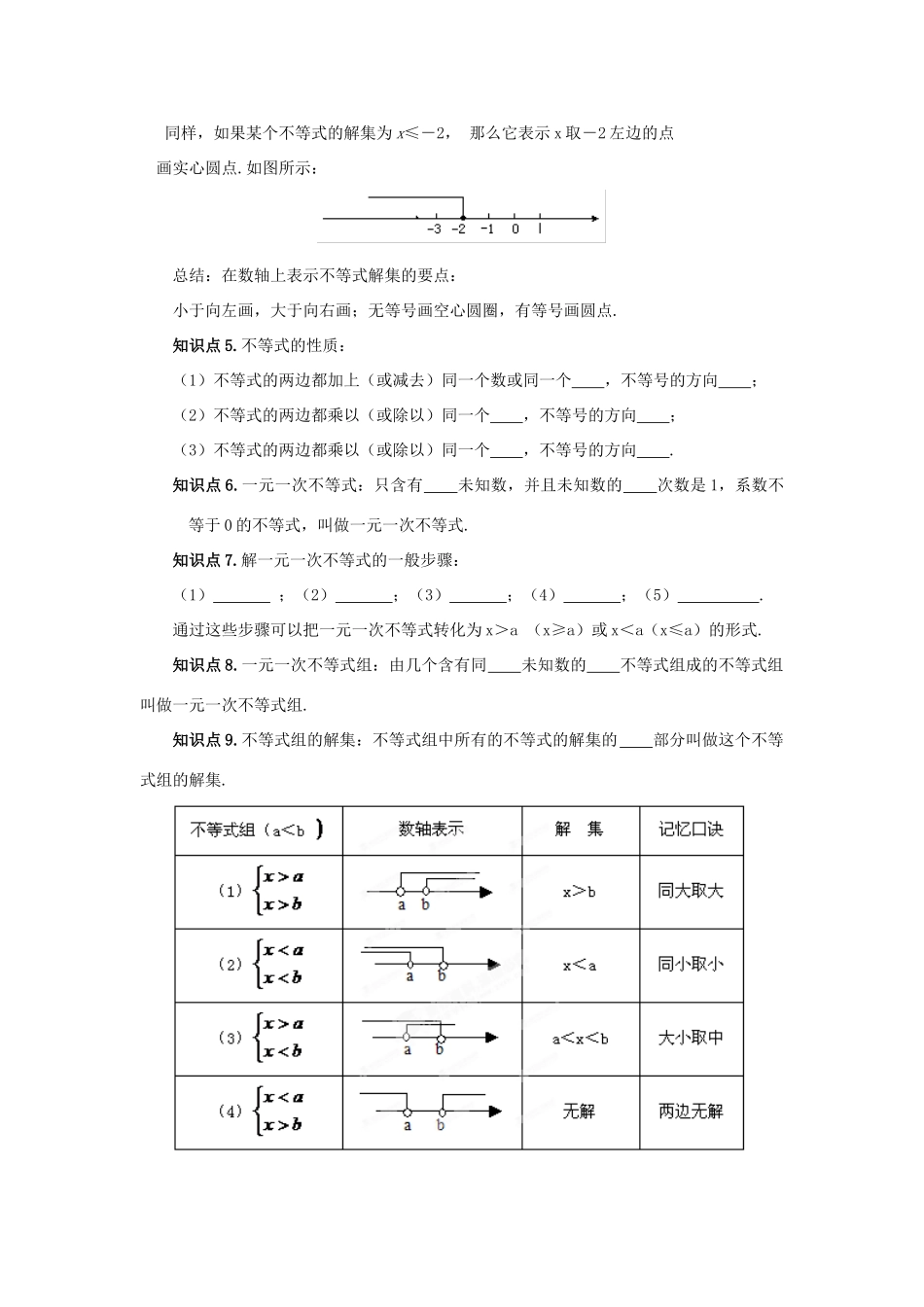
2.2一次不等式(组)复习教案教学目标:1.会用不等式的基本性质解不等式(组).(重点)2.会在数轴上表示不等式(组)的解集.3.能利用不等式(组)解决生活中的实际问题.(难点)教法及学法指导:教法:1.创设情境法.通过展示导学案,创设问题情境,激发学生学习兴趣.2.设疑启发法.通过设置疑问,启学生思维,引导学生分析问题.学法:1.自主探索法.学生通过独立思考,探索分析,提高数学分析能力.2.合作学习法.学生通过小组讨论,交流等学习过程,加强合作交流,提高学习效果.课前准备:教师准备:课件、导学案、三角板.学生准备:尝试完成导学案.教学过程:一、知识要点梳理(导学案提前下发,学生在导学案中填空.)知识点1.不等式的定义:用连接的式子叫做不等式.知识点2.不等式的解:能使不等式成立的的值叫做不等式的解.知识点3.不等式的解集:一个含有未知数的不等式的叫做这个不等式的解集.知识点4.不等式的解集在数轴上的表示:(1)x>a:数轴上表示a的点画成圆圈,表示a的点的边部分来表示;(2)x<a:数轴上表示a的点画成圆圈,表示a的点的边部分来表示;(3)x≥a:数轴上表示a的点画成圆点,表示a的点及表示a的点的边部分来表示;(4)x≤a:数轴上表示a的点画成圆点,表示a的点及表示a的点的边部分来表示.例如:在数轴上表示大于3的数的点应该是数3所对应点的右边。画图时要注意方向(向右)和端点(不包括数3,在对应点画空心圆圈).如图所示:同样,如果某个不等式的解集为x≤-2,那么它表示x取-2左边的点画实心圆点.如图所示:总结:在数轴上表示不等式解集的要点:小于向左画,大于向右画;无等号画空心圆圈,有等号画圆点.知识点5.不等式的性质:(1)不等式的两边都加上(或减去)同一个数或同一个,不等号的方向;(2)不等式的两边都乘以(或除以)同一个,不等号的方向;(3)不等式的两边都乘以(或除以)同一个,不等号的方向.知识点6.一元一次不等式:只含有未知数,并且未知数的次数是1,系数不等于0的不等式,叫做一元一次不等式.知识点7.解一元一次不等式的一般步骤:(1);(2);(3);(4);(5).通过这些步骤可以把一元一次不等式转化为x>a(x≥a)或x<a(x≤a)的形式.知识点8.一元一次不等式组:由几个含有同未知数的不等式组成的不等式组叫做一元一次不等式组.知识点9.不等式组的解集:不等式组中所有的不等式的解集的部分叫做这个不等式组的解集.知识点10.解不等式组:求不等式组解集的叫做解不等式组.知识点11.解一元一次不等式组的一般步骤:先分别求出不等式组中的各个不等式的,然后再求出这几个不等式解集的部分.知识点12.列不等式(组)解应用题的一般步骤:审题、设、找、列、解、检验作答.(展台展示一生的导学案,学生检查并纠正错误.多媒体展示标准答案.)1.不等号2.未知数3.解的全体4.空心、右、空心、左、实心、左、实心、右5.整式、不变、正数、不变、负数、改变6.一个、最高7.去分母;去括号;移项;合并同类项;未知数的系数化为1.8.一个、一次9.公共10.过程11.解集、公共12.未知数、不等关系、不等式(组)、不等式(组).设计意图:在填空的过程中,让学生初步回顾本章学习的内容,如有遗忘,借用课本或同学间交流进行补充.这样做既可以节省课上时间,也能为知识网络图的理解做准备.实际效果:主要存在以下几个方面的问题:①语言不严密,概念把握不准;②不等式的性质第三条不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变学生没记清楚;③学生的书写不整洁的太多等.通过上课时展示,学生间相互找问题,能够将语言规范.这样做能够曝露出学生掌握存在的问题,比直接说更能感悟到知识的严密性,同时也节省了上课的时间.师:这节课我们将再一次走进不等式(组),进一步探究其中蕴含的数学思想及方法.(教师板书课题)请同学们结合下列知识网络图对本章内容进行简要回顾.(教师留给学生3分钟时间,让学生明白本章知识及知识间的联系.)二.本章知识结构图(多媒体投影展示)三.基础知识训练(一)不等式的基本性质的应用1.已知a﹤b,下列式子不成立的是()A.﹤B.﹤C.﹥D.如果﹤0,那么﹤.2.解不等式组师...