二次函数与角度一VIP免费

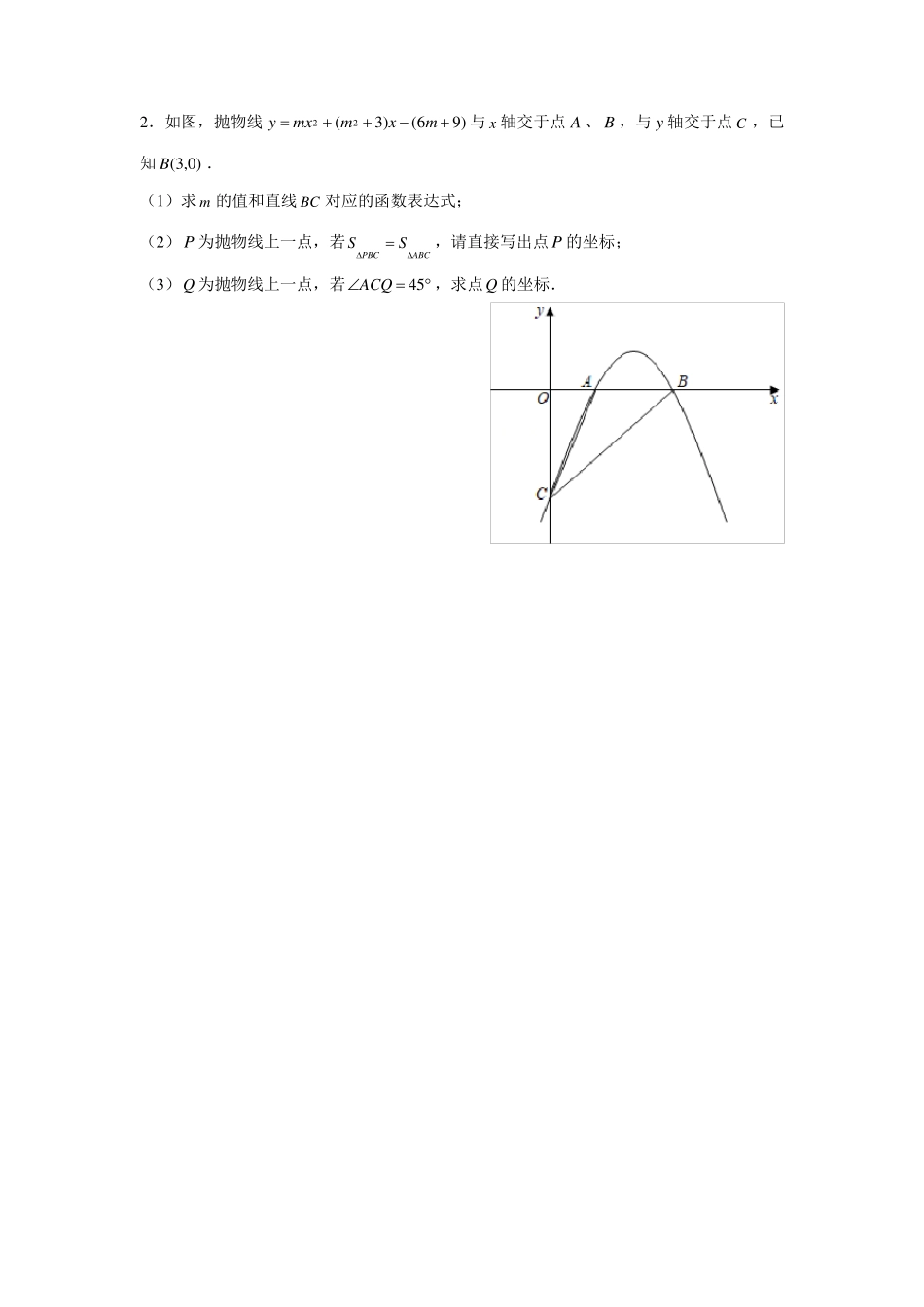
二次函数与角度（一）1．如图，抛物线y(x1)(xa)（其中a1)与x轴交于A、B两点，交y轴于点C．（1）直接写出OCA的度数和线段AB的长（用a表示）；（2）若点D为ABC的外心，且BCD与ACO的周长之比为10:4，求此抛物线的解析式；（3）在（2）的前提下，试探究抛物线y(x1)(xa)上是否存在一点P，使得CAPDBA？若存在，求出点P的坐标；若不存在，请说明理由．2．如图，抛物线ymx2(m23)x(6m9)与x轴交于点A、B，与y轴交于点C，已知B(3,0)．（1）求m的值和直线BC对应的函数表达式；（2）P为抛物线上一点，若SPBCSABC，请直接写出点P的坐标；（3）Q为抛物线上一点，若ACQ45，求点Q的坐标．3．如图，在平面直角坐标系xOy中，抛物线ya(xh)2k与x轴相交于O，A两点，顶点P的坐标为(2,1)．点B为抛物线上一动点，连接AP，AB，过点B的直线与抛物线交于另一点C．（1）求抛物线的函数表达式；（2）若点B的横坐标与纵坐标相等，ABCOAP，且点C位于x轴上方，求点C的坐标；（3）若点B的横坐标为t，ABC90，请用含t的代数式表示点C的横坐标，并求出当t0时，点C的横坐标的取值范围．4．二次函数yax2bx4(a0)的图象经过点A(4,0)，B(1,0)，与y轴交于点C，点P为第二象限内抛物线上一点，连接BP、AC，交于点Q，过点P作PDx轴于点D．（1）求二次函数的表达式；（2）连接BC，当DPB2BCO时，求直线BP的表达式；（3）请判断：PQ是否有最大值，如有请求出有最大值时点P的坐标，如没有请说明理由．QB5．如图，已知抛物线yax2bx4(a0)与x轴交于点A(1,0)和B，与y轴交于点C，对称轴为直线x5．2（1）求抛物线的解析式；（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ，当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由；（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且DQE2ODQ．在y轴上是否存在点F，使得BEF为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．6．如图，在平面直角坐标系中，已知抛物线yax2bx4(a0)经过点A(2,0)和点B(4,0)．（1）求这条抛物线所对应的函数表达式；（2）点P为该抛物线上一点（不与点C重合），直线CP将ABC的面积分成2:1两部分，求点P的坐标；（3）点M从点C出发，以每秒1个单位的速度沿y轴移动，运动时间为t秒，当OCAOCBOMA时，求t的值．7．如图，抛物线yax2bx2经过A(1,0)，B(4,0)两点，与y轴交于点C，连接BC．（1）求该抛物线的函数表达式；（2）如图2，直线l:ykx3经过点A，点P为直线l上的一个动点，且位于x轴的上方，点Q为抛物线上的一个动点，当PQ//y轴时，作QMPQ，交抛物线于点M（点M在点，以PQ，QM为邻边构造矩形PQMN，求该矩形周长的最小值；Q的右侧）（3）如图3，设抛物线的顶点为D，在（2）的条件下，当矩形PQMN的周长取最小值时，抛物线上是否存在点F，使得CBFDQM？若存在，请求出点F的坐标；若不存在，请说明理由．8．已知二次函数yax2bxc(a0)．（1）若a1，bc2，求方程ax2bxc0的根的判别式的值；2（2）如图所示，该二次函数的图象与x轴交于点A(x1，0)、B(x2，0)，且x10x2，与yb轴的负半轴交于点C，点D在线段OC上，连接AC、满足ACOABD，BD，cx1．a①求证：AOCDOB；②连接BC，过点D作DEBC于点E，点F(0,x1x2)在y轴的负半轴上，连接AF，且ACOCAFCBD，求c的值．x119．如图，抛物线yx2bxc与x轴交于A(1,0)，B(4,0)，与y轴交于点C．连接AC，2BC，点P在抛物线上运动．（1）求抛物线的表达式；（2）如图①，若点P在第四象限，点Q在PA的延长线上，当CAQCBA45时，求点P的坐标；（3）如图②，若点P在第一象限，直线AP交BC于点F，过点P作x轴的垂线交BC于点H，当PFH为等腰三角形时，求线段PH的长．10．如图，已知抛物线yax2bx5(a0)与x轴交于点A(5,0)，点B(1,0)（点A在点B15的左边），与y轴交于点C，点D为抛物线的顶点，连接BD．直线yx经过点A，22且与y...