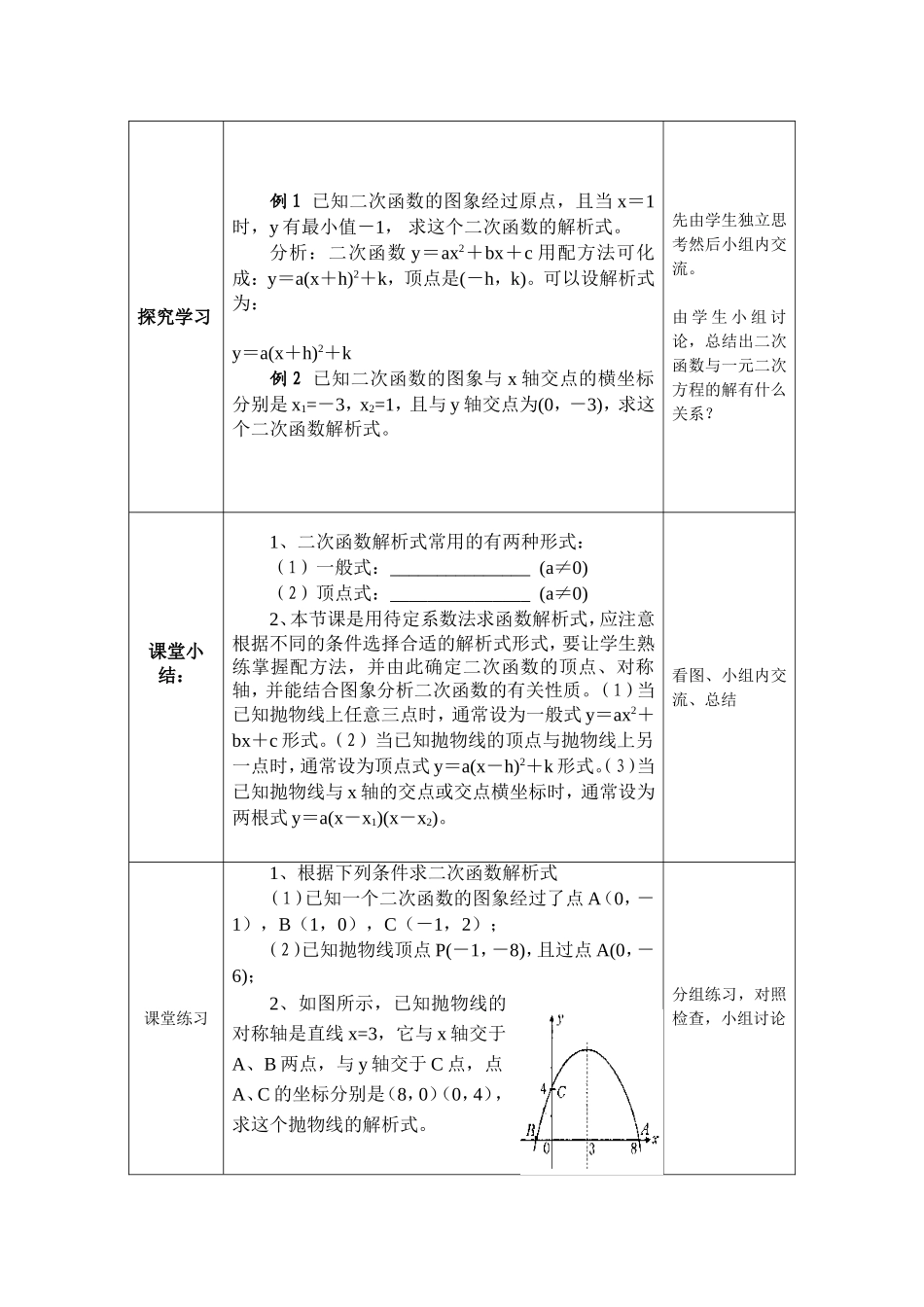
课题:用待定系数法求二次函数解析式学科组数学年级九年级设计人喻乾丽上课时间教学目标1、通过对用待定系数法求二次函数解析式的探究,掌握求解析式的方法。2、能灵活的根据条件恰当地选取选择解析式,体会二次函数解析式之间的转化。3、从学习过程中体会学习数学知识的价值,从而提高学习数学知识的兴趣。教学重点能灵活的根据条件恰当地选取选择解析式,体会二次函数解析式之间的转化。教学难点进一步培养学生综合解题能力,渗透数形结合的思想是教学的难点.教学准备三角板、铅笔、小黑板教学环节问题情境(教师活动)学生活动情境导入:1、二次函数解析式常用的有两种形式:(1)一般式:_______________(a≠0)(2)顶点式:_______________(a≠0)先独立思考然后小组讨论探究学习例1已知二次函数的图象经过原点,且当x=1时,y有最小值-1,求这个二次函数的解析式。分析:二次函数y=ax2+bx+c用配方法可化成:y=a(x+h)2+k,顶点是(-h,k)。可以设解析式为:y=a(x+h)2+k例2已知二次函数的图象与x轴交点的横坐标分别是x1=-3,x2=1,且与y轴交点为(0,-3),求这个二次函数解析式。先由学生独立思考然后小组内交流。由学生小组讨论,总结出二次函数与一元二次方程的解有什么关系?课堂小结:1、二次函数解析式常用的有两种形式:(1)一般式:_______________(a≠0)(2)顶点式:_______________(a≠0)2、本节课是用待定系数法求函数解析式,应注意根据不同的条件选择合适的解析式形式,要让学生熟练掌握配方法,并由此确定二次函数的顶点、对称轴,并能结合图象分析二次函数的有关性质。(1)当已知抛物线上任意三点时,通常设为一般式y=ax2+bx+c形式。(2)当已知抛物线的顶点与抛物线上另一点时,通常设为顶点式y=a(x-h)2+k形式。(3)当已知抛物线与x轴的交点或交点横坐标时,通常设为两根式y=a(x-x1)(x-x2)。看图、小组内交流、总结课堂练习1、根据下列条件求二次函数解析式(1)已知一个二次函数的图象经过了点A(0,-1),B(1,0),C(-1,2);(2)已知抛物线顶点P(-1,-8),且过点A(0,-6);2、如图所示,已知抛物线的对称轴是直线x=3,它与x轴交于A、B两点,与y轴交于C点,点A、C的坐标分别是(8,0)(0,4),求这个抛物线的解析式。分组练习,对照检查,小组讨论课后反思