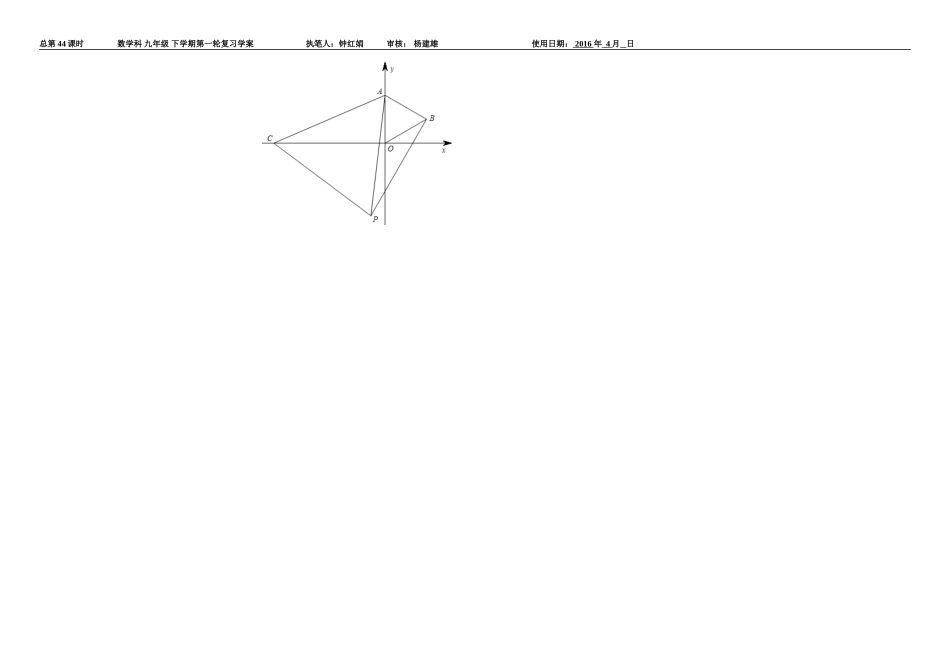
总第44课时数学科九年级下学期第一轮复习学案执笔人:钟红娟审核:杨建雄使用日期:2016年4月日第四单元:《三角形》测验班别:姓名:成绩:一、选择题(每小题3分,共24分)1.已知∠A是锐角,且sinA=,那么∠A等于()A.30°B.45°C.60°D.75°2.下列命题中,是真命题的为()(A)锐角三角形都相似(B)直角三角形都相似(C)等腰三角形都相似(D)等边三角形都相似.3.如图,BE、CD相交于点O,且∠l=∠2,图中有几组相似三角形()A.2组B.3组C.4组D.5组4.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是()(A)5(B)6(C)11(D)165.如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于()(A)60m(B)40m(C)30m(D)20m6.如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF()A.AC∥DFB.∠A=∠DC.AC=DFD.∠ACB=∠F第6题图7.一个等腰三角形的两边长分别是3和7,则它的周长为()A.17B.15C.13D.13或178.在中,,,.则点到的距离是()(A)(B)(C)(D)二、填空题(每小题5分,共30分)9.如图,在△ABC中,D,E分别是边AB,AC的中点,若BC=6,则DE=_________.10如图是一副三角板叠放的示意图,则∠α=.11.如图,BD是的角平分线,,则图中的等腰三角形有____个.12.点P在线段AB的垂直平分线上,PA=7,则PB=______________.13.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25米,那么这根旗杆的高度为__________m14.如图,在等腰中,=90°,OA=1,以OA1为直角边作等腰,以OA2为直角边作等腰,…,则OAn的长度为第9题第10题第11题三、解答题(每小题8分,共24分)15.计算:sin230O+cos245O+sin60Otan45O16.如图,△ABO的坐标分别为A(1,3),B(3,2),O(0,0),画一个△A′B′O′,使它以原点O为位似中心,与△ABO的位似比等于2:1.并写出△A′B′O′的各顶点坐标。第14题图AA1A2A3A4OADCBADBCACDB总第44课时数学科九年级下学期第一轮复习学案执笔人:钟红娟审核:杨建雄使用日期:2016年4月日17.如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB,求证:∠A=∠E四、解答题:(18-21每题10分,22题12分共42分)18.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.(1)求证:△ACD∽△CDB(2)若AD=1,BD=4,求CD的长。19.如图,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14米到达D,在D处测得A的仰角为60°,求铁塔AB的高。20.如图10,,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G。(1)求证:△ADE≌△CFE;(2)若GB=2,BC=4,BD=1,求AB的长。21.如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.(1)求AD的长;(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;22.如图,在直角坐标系中,点A的坐标是(0,3),点C是x轴上的一个动点,点C在x轴上移动时,始终保持△ACP是等边三角形.当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).(1)点C在移动的过程中,当等边三角形ACP的顶点P在第三象限时(如图所示),求证:△AOC≌△ABP;由此你发现什么结论?(2)求点C在x轴上移动时,点P所在函数图象的解析式.总第44课时数学科九年级下学期第一轮复习学案执笔人:钟红娟审核:杨建雄使用日期:2016年4月日