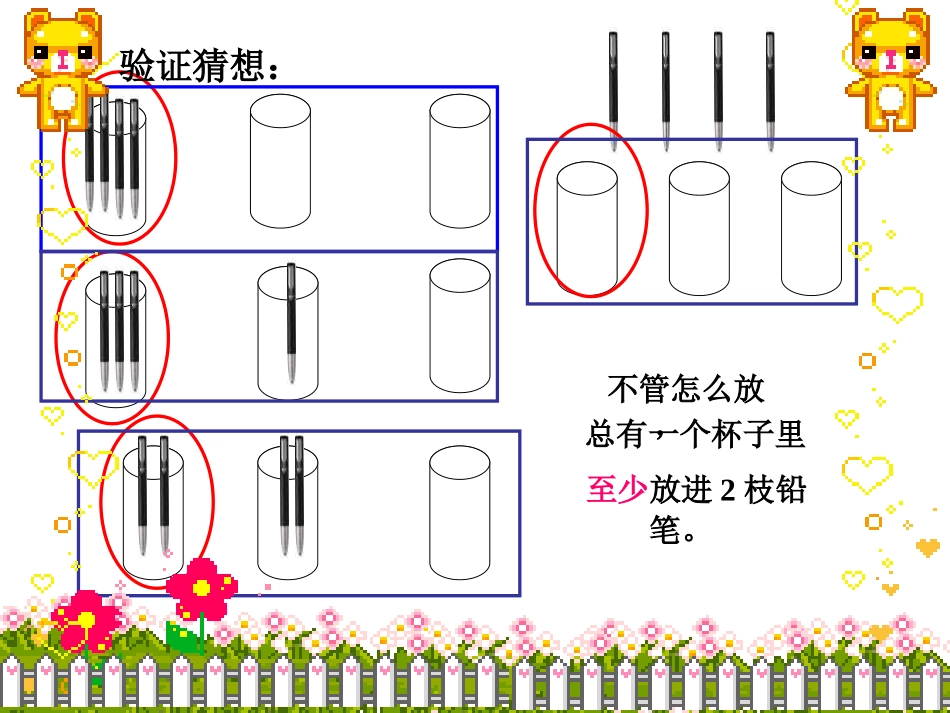
例1:把4枝铅笔放进3个杯子里猜想:1、应该怎么放,有多少种放法?2、比较这几种放法,你有什么发现?至少放进2枝铅笔。不管怎么放,总有一个杯子里验证猜想:那么把5枝铅笔放进4个杯子里,会怎样呢?那么把6枝铅笔放进5个杯子里,会怎样呢?那么把7枝铅笔放进6个杯子里,会怎样呢?那么把100枝铅笔放进99个杯子里,会怎样呢?优化练习发现规律1:当铅笔的枝数比杯子数多1时,不管怎么放,总有一个杯子里至少放2枝铅笔。例2:把7枝铅笔放进3个杯子里,不管怎么放,总有一个杯子至少放几枝铅笔?(用式子怎么表示?)7÷3=2…..1把8枝铅笔放进3个杯子里,不管怎么放,总有一个杯子至少放几枝铅笔?(用式子怎么表示?)把8枝铅笔放进2个杯子里不管怎么放,总有一个杯子至少放几枝铅笔?(用式子怎么表示?)8÷3=2….28÷2=4(2+1=3)(至少数)(2+1=3)(至少数)4(至少数)发现规律2:物体的数量大于抽屉(杯子)的数量,总有一个抽屉(杯子)里至少放进了商加1个物体。实践应用,拓展延伸。从扑克牌中取出两张王牌,从剩下的52张中任意抽出5张,至少有几张是同花色的。试一试,并说明理由。课堂练习:一:填空题1、9个小朋友分10块糖,总有一个小朋友至少分()块糖。2、将85个苹果分给84名学生,总有()名学生分()个苹果。3、15个梨放入6个盘子,总有()个盘子至少放()个梨。4、将64个橘子分给8个小朋友,不管怎么分,总有1个小朋友至少分()个橘子。212138二、判断题1、在任意37人中,至少有4人的属相相同。()2、从数1、2、3‥‥‥10中任取6个数,这六个数中既有奇数也有偶数。()三、拓展思维盒子里有同样大小的红球和蓝球各4个。要想摸出的球一定有2个同色的,最少要摸出几个球?√√课堂小结:通过今天的学习你有什么收获?赠:一一一一一一一一一一一一一一一一一一一