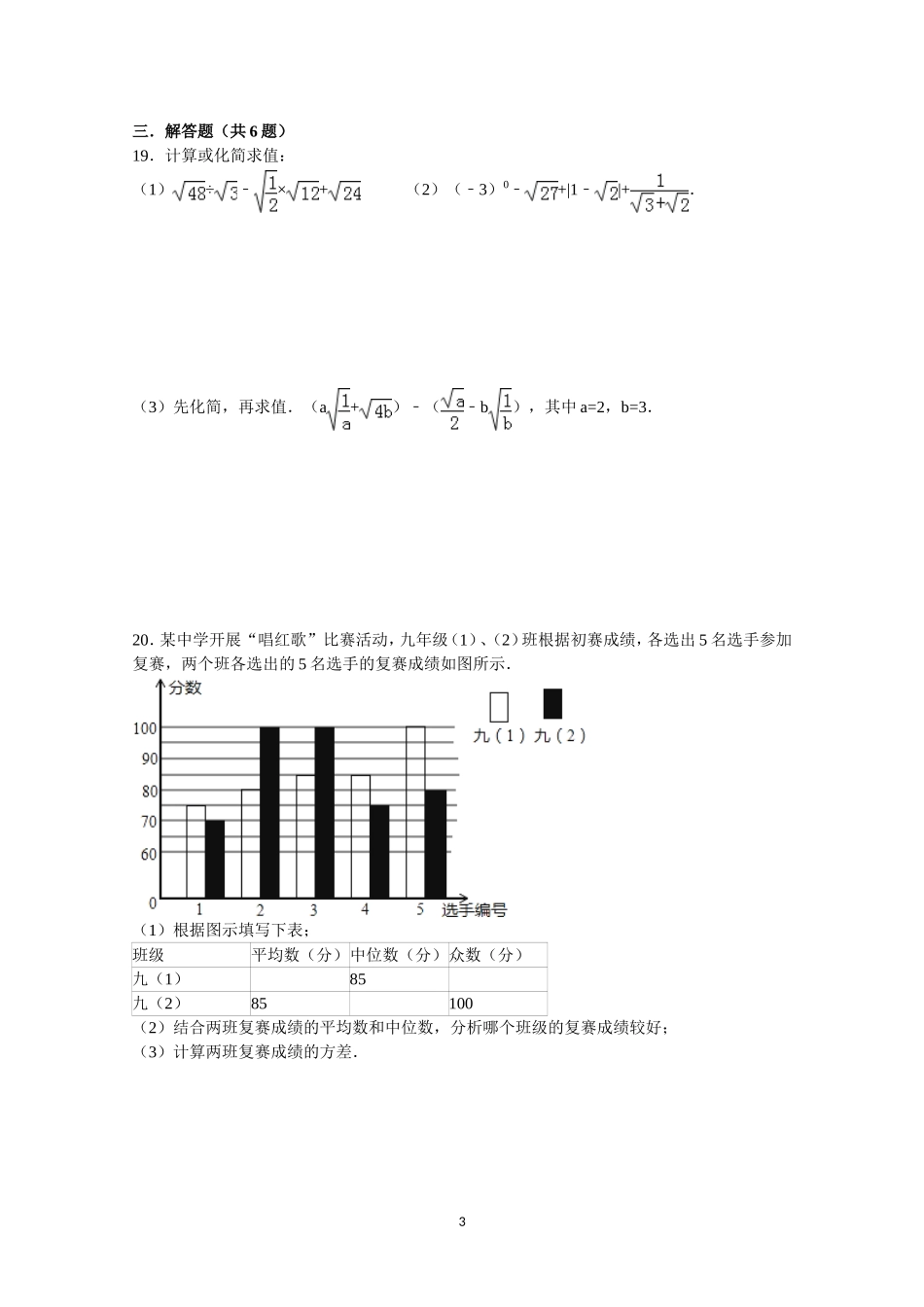
2016年八年级下册期末数学测试题一.选择题(共12小题)1.若a为实数,则化简的结果是()A.a﹣B.aC.±aD.|a|2.函数y=中自变量x的取值范围是()A.x>﹣1且x≠2B.x≥1﹣C.x≠1﹣D.x>﹣13.如图,∠ABC=90°,AB=6,BC=8,AD=CD=7,若点P到AC的距离为5,则点P在四边形ABCD边上的个数为()A.0B.2C.3D.4第3题图第4图第5题图第6题图4.如图,在RtABC△中,∠C=90°,D为BC上的一点,AD=BD=2,AB=,则AC的长为()A.B.C.3D.5.如图,△ABC中,D,E分别上边AB,AC的中点,若DE=3,则BC=()A.B.9C.6D.56.如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,DCFE是平行四边形,则图中阴影部分的面积为()A.3B.4C.6D.87.甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示.下列关于此次赛跑说法正确的是()A.乙比甲跑的路程多B.这是一次100米赛跑C.甲乙同时到达终点D.甲的速度为8m/s8.函数y=kx+b(k≠0)中,当x的值增加2时,y的值减小3,则k的值为()A.﹣B.﹣C.2﹣D.3﹣9.对每个x,y是y1=2x,y2=x+2,y3=﹣x+12三个值中的最小值,则当x变化时,函数y的最大值是()A.4B.5C.6D.7110.如图,把RtABC△放在平面直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0),(8,0),将△ABC沿x轴向右平移,当点C落在直线y=2x4﹣上时,线段BC扫过的面积为()A.8B.16C.16D.32第10题图第12题图第15题图第16题图11.如果一次函数y=x+1﹣的图象与x轴、y轴分别交于点A点、B点,点M在x轴上,并且使以点A、B、M为顶点的三角形是等腰三角形,那么这样的点M有()A.3个B.4个C.5个D.7个12.在正方形ABCD中,P为AB的中点,BEPD⊥的延长线于点E,连接AE、BE、FAAE⊥交DP于点F,连接BF,FC.下列结论:①△ABEADF△;②FB=AB;③CFDP⊥;④FC=EF其中正确的是()A.①②④B.①③④C.①②③D.①②③④二.填空题(共6小题)13.学校篮球队五名队员的年龄分别为17,15,17,16,15,其方差为0.8,则三年后这五名队员年龄的方差为.14.若x、y为实数,且y=++3,则yx的值为.15.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=.16.如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为.17.已知点P(a,b)在直线上,点Q(﹣a,2b)在直线y=x+1上,则代数式a24b﹣21=﹣.18.如图,直线y=2x+8与x,y轴分别交于A,B两点,以OB为底边在y轴右侧作等腰三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为.2三.解答题(共6题)19.计算或化简求值:(1)÷﹣×+(2)(﹣3)0﹣+|1﹣|+.(3)先化简,再求值.(a+)﹣(﹣b),其中a=2,b=3.20.某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.(1)根据图示填写下表;班级平均数(分)中位数(分)众数(分)九(1)85九(2)85100(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;(3)计算两班复赛成绩的方差.321.如图,在四边形ABCD中,AB=1,BC=1,CD=2,DA=,且∠ABC=90°,求四边形ABCD的面积.22.已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:(1)AE=AB;(2)如果BM平分∠ABC,求证:BMCE⊥.423.如图1所示,已知温沪动车铁路上有A、B、C三站,B、C两地相距280千米,甲、乙两列动车分别从B、C两地同时沿铁路匀速相向出发向终点C、B站而行,甲、乙两动车离A地的距离y(千米)与行驶时间表x(时)的关系如图2所示,根据图象,解答以下问题:(1)填空:路程a=,路程b=.点M的坐标为.(2)求动车甲离A地的距离y甲与行驶时间x之间的函数关系式.(3)补全动车乙的大致的函数图象.(直接画出图象)524.如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.(1)求直线AC的函数关系式;(2)连接BM,动点P从点A出发,沿折线ABC﹣﹣方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围).6