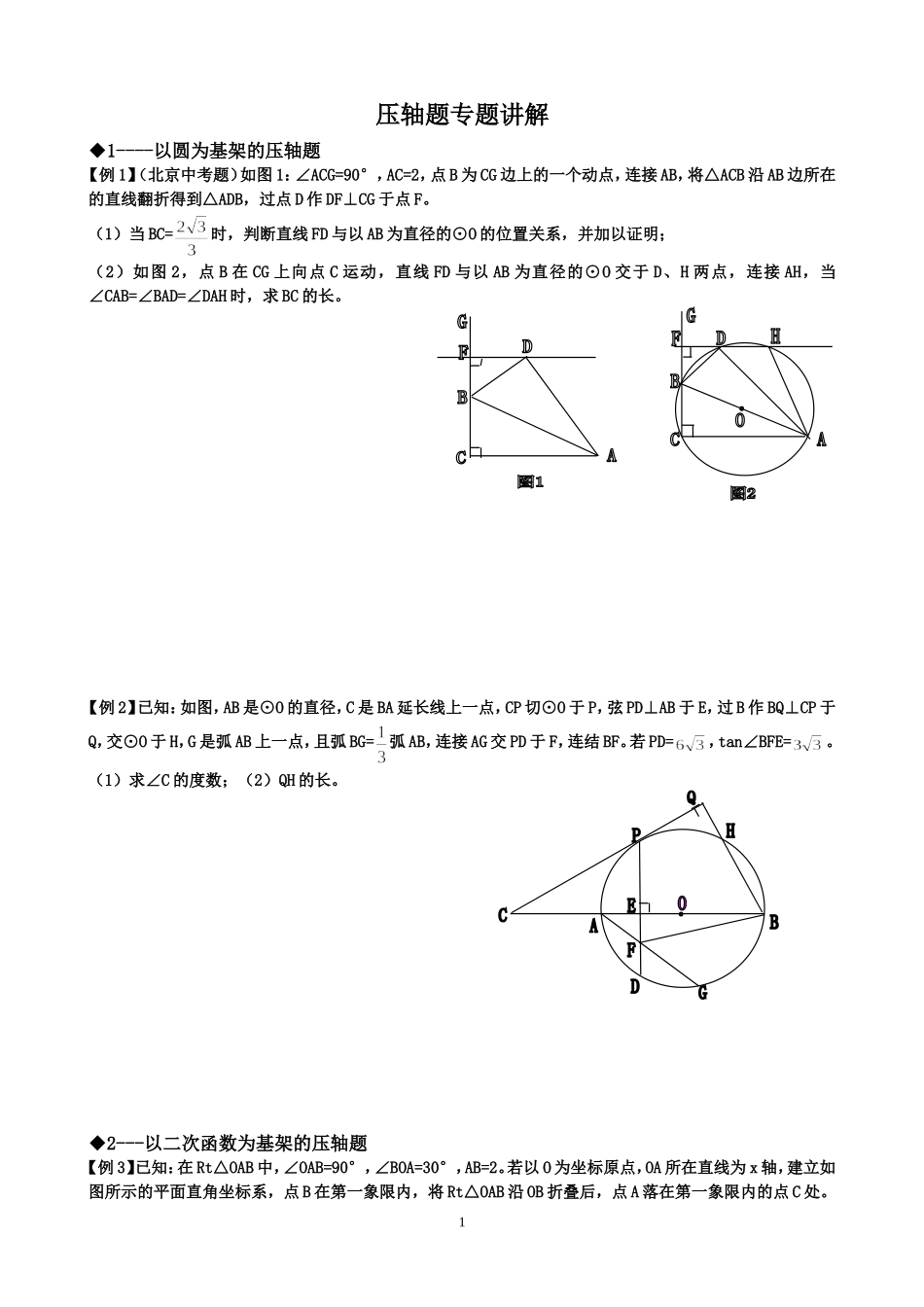
1压轴题专题讲解◆1----以圆为基架的压轴题【例1】(北京中考题)如图1:∠ACG=90°,AC=2,点B为CG边上的一个动点,连接AB,将△ACB沿AB边所在的直线翻折得到△ADB,过点D作DF⊥CG于点F。(1)当BC=时,判断直线FD与以AB为直径的⊙O的位置关系,并加以证明;(2)如图2,点B在CG上向点C运动,直线FD与以AB为直径的⊙O交于D、H两点,连接AH,当∠CAB=∠BAD=∠DAH时,求BC的长。【例2】已知:如图,AB是⊙O的直径,C是BA延长线上一点,CP切⊙O于P,弦PD⊥AB于E,过B作BQ⊥CP于Q,交⊙O于H,G是弧AB上一点,且弧BG=弧AB,连接AG交PD于F,连结BF。若PD=,tan∠BFE=。(1)求∠C的度数;(2)QH的长。◆2---以二次函数为基架的压轴题【例3】已知:在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2。若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。2(1)求点C的坐标;(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。【例4】如图:点O是原点,A(n,0)是x轴上一动点(n﹤0),以AO为一边作矩形AOBC,使OB=2OA,点C在第二象限,将矩形AOBC绕点A逆时针旋转90°得矩形AGDE,过点A的直线y=kx+m交y轴于点F,FB=FA,抛物线y=ax2+bx+c过点E、F、G,且和直线交于点H,过点H作x轴的垂线,垂足为M。①求k的值;②点A的位置改变时,△AMH的面积和矩形AOBC的面积的比是否改变?说明你的理由。◆3---方程、函数的综合【例5】如图:直线与x轴、y轴分别交于点B、C,以点A(1,0)为圆心,以AB的长为半径作⊙A,分别交x轴、y轴的正半轴于点D、E,直线m与⊙A交于点F,分别过点B、F作⊙A的切线交于点M。(1)直接写出点B、C的坐标;(2)求直线MF的解析式;3(3)若点P是上任意一点(不与B、F重合)连结BP、FP,过点M作MN∥PF,交直线m于点N,设PB=a,MN=b,求b与a的函数关系式,并写出自变量a的取值范围;(4)若将(3)中的条件点P是上任意一点,改为P是⊙A上任意一点,其他条件不变,当点P在⊙A上的什么位置时,△BMN为直角三角形,并写出此时点N的坐标;【例6】如图:对称轴为直线X=7/2的抛物线经过点A(6,0)和B(0,4)。(1)求抛物线的解析式及顶点坐标;(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形。求平行四边形OEAF的面积S与X之间的函数关系式,并写出自变量X的取值范围;①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由。【例7】直线L与轴交于点P(1,0),与轴所夹的锐角为,且,直线L与抛物线相交于点B(,-3)与D(3,),(1)求B.D两点的坐标,并用含的代数式表示和;(2)①若关于的方程有实数根,求此抛物线的解析式;②若抛物线与轴相交于A.C两点,顺次连结A.B.C.D得凸四边形ABCD,问:四边形ABCD的面积S有无最大值或最小值?若有,求S的最大值或最小值;若没有,请说明理由。4ABCyxOQDEABCyxOH【例8】如图,抛物线()与轴交于点(,),与轴交于点、,点的坐标为(,)。(1)求该抛物线的解析式;(2)点是线段上的动点,过点作,交于点,连接。当的面积最大时,求点的坐标;(3)若平行于轴的动直线与该抛物线交于点,与直线交于点,点的坐标为(,)。问:是否存在这样的直线,使得是等腰三角形?若存在,请求出点的坐标;若不存在,请说明理由。家庭作业1、在平面直角坐标系中,抛物线与轴的两个交点分别为(,)、(1,),过顶点作轴于点.(1)直接填写:;;顶点的坐标为;(2)在轴上是否存在点,使得是以为斜边的直角三角形?若存在,求出点的坐标;若不存在,说明理由;(3)若点为轴上方的抛物线上一动点(点与顶点不重合),于点,当与相似时,求点的坐标。LDCPOBAyxθ5BAOyPxM2、二次函数的图象交轴...