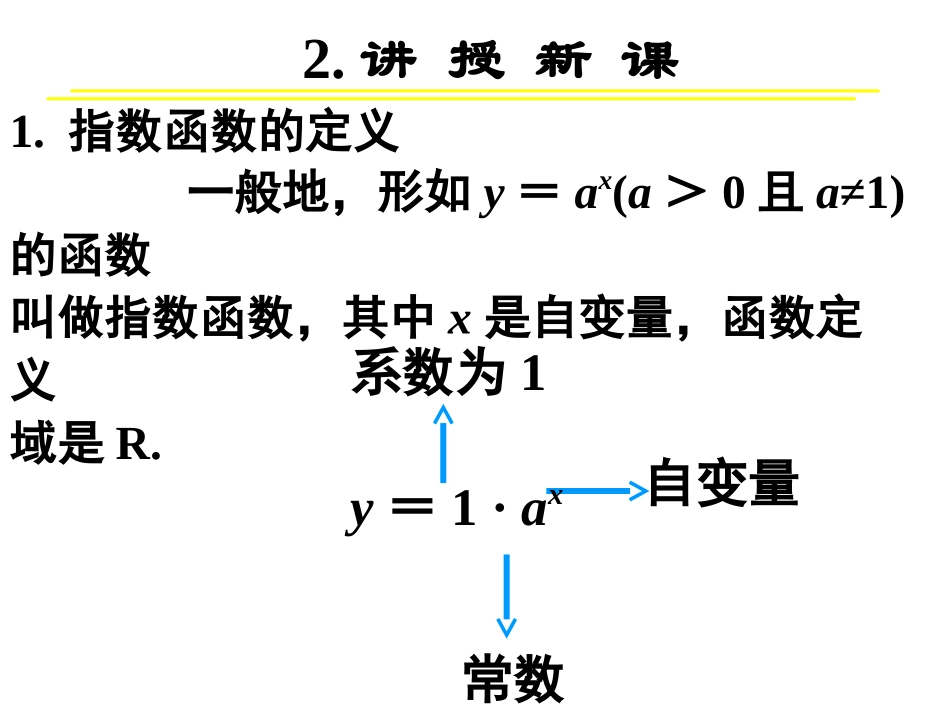
1.引入传说西塔发明了国际象棋而使国王十分高兴,他决定要重赏西塔,西塔说:“只要你在我的棋盘上赏一些麦子就行了。在棋盘的第1个格子里放1粒,在第2个格子里放2粒,依此类推,以后每一个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到放满第64个格子就行了”。计数麦粒的工作开始了,但还没有到第二十格,一袋麦子已经空了。国王很快就看出,即便拿出全国的粮食,也兑现不了他对西塔的诺言。事实上所需麦粒总数为:18446744073709551615,这些麦子有多少?打个比方,如果造一个高4公尺宽10公尺的仓库来放这些麦子,那么仓库的长度就等于地球到太阳的距离的两倍。而要生产这么多的麦子,全世界要两千年。1.指数函数的定义常数自变量系数为12.讲授新课y=1·ax一般地,形如y=ax(a>0且a≠1)的函数叫做指数函数,其中x是自变量,函数定义域是R.讲授新课(3)若a=1,则y=ax=1是一个常数函数.(1)若a=0,则当x>0时,ax=0;当x=0时,ax无意义;当x<0时,ax无意义.(2)若a<0,则ax没有意义.2对常数a的限制条件:⑴y=10x;⑵y=10x+1;⑶y=10x+1;⑷y=2·10x;⑸y=(-10)x;⑹y=(10+a)x(a>-10,且a≠-9);(3)课堂练习:例1.下列函数是指数函数?请放入集合A中.⑹y=(10+a)x(a>-10,且a≠-9)⑴y=10x;集合A:3.指数函数的图象和性质:几何画板几何画板结论:(2)a>1时,指数函数单调递增0<a<1时,指数函数单调递减.(1)定义域:值域:定点:(0,1)R(0,)课堂小结1.指数函数的概念;2.指数函数的图象和性质.a>10
0时,x≤0时,x>0时,x≤0时,11xxOOyy指数函数f(x)=ax(a>0,且a≠1)的图象和性质:R(0,1)递增递减y>10>>1;1的365次方=1;0.99的365次方=0.02551796445229<<<1;1.01=1+0.01,也就是每天进步一点,1.01的365次方也就是说你每天进步一点,一年以后,你将进步很大,远远大于“1”;勿以善小而不为.1是指原地踏步,一年以后你还是原地踏步,还是那个“1”.0.99=1-0.01,也就是说你每天退步一点点,你将在一年以后,远远小于“1”,远远被人抛在后面,将会是“1”事无成;因此勿以恶小而为之,勿以善小而不为.作业:教材P59,7.8题教材P59,7.8题课后思考题“孙悟空的金箍棒长1.5米,他喊一声变,就将金箍棒长变成原来的2倍,那么孙悟空喊多少声就能使棒变得比珠穆朗玛峰高?”感谢各位领导,老师和同学们请多多指导教材P57页例7.比较下列各题中两个值的大小①1.72.5,1.73;②0.8-0.1,0.8-0.2;③1.70.3,0.93.1.利用图像的单调性比较数值的大小利用图像的单调性比较数值的大小小结:①底数相同时,可利用指数函数的单调性判断;②指数相同时可由图像的变化规律判断;③底数和指数均不同时,寻找中间值1(即底数的0次幂)判断.小结:①底数相同时,可利用指数函数的单调性判断;②指数相同时可由图像的变化规律判断;③底数和指数均不同时,寻找中间值1(即底数的0次幂)判断.