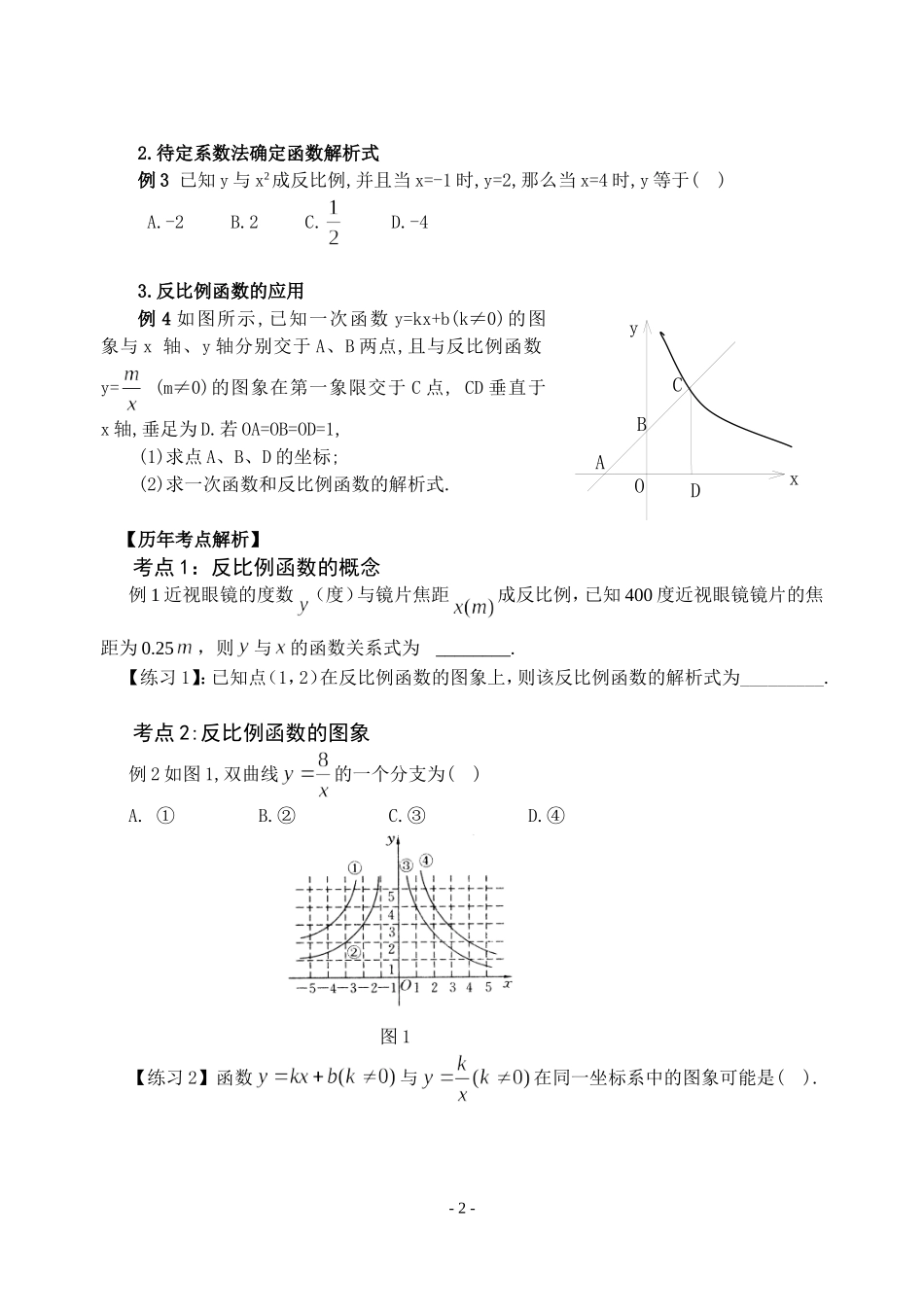
反比例函数复习课【中考知识点】1.反比例函数意义;2.反比例函数反比例函数图象;3.反比例函数性质;4.待定系数法确定函数解析式.【基础知识梳理】1.反比例函数的概念反比例函数y=中的是一个分式,自变量x≠0,函数与x轴、y轴无交点,y=也可写成y=kx-1(k≠0),注意自变量x的指数为-1,在解决有关自变量指数问题时应特别注意系数k≠0这一限制条件.2.反比例函数的图象在用描点法画反比例函数y=的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.3.反比例函数y=中k的意义注意:反比例函数y=(k≠0)中比例系数k的几何意义,即过双曲线y=(k≠0)上任意一点引x轴、y轴垂线,所得矩形面积为│k│.4.反比例函数经常与一次函数、二次函数等知识相联系.【例题解析】1.反比例函数的图象例1函数y=(x>0)的图象大致是()例2函数y=kx+1与函数y=在同一坐标系中的大致图象是()-1-yOxAyOxByOxCyOxDyOxAyOxByOxCyOxD2.待定系数法确定函数解析式例3已知y与x2成反比例,并且当x=-1时,y=2,那么当x=4时,y等于()A.-2B.2C.D.-43.反比例函数的应用例4如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1,(1)求点A、B、D的坐标;(2)求一次函数和反比例函数的解析式.【历年考点解析】考点1:反比例函数的概念例1近视眼镜的度数(度)与镜片焦距成反比例,已知400度近视眼镜镜片的焦距为0.25,则与的函数关系式为________.【练习1】:已知点(1,2)在反比例函数的图象上,则该反比例函数的解析式为_________.考点2:反比例函数的图象例2如图1,双曲线的一个分支为()A.①B.②C.③D.④图1【练习2】函数与在同一坐标系中的图象可能是().-2-yOxDCBAABCD考点3.反比例函数的性质例3若、、三点都在函数的图象上,则的大小关系是()A.B.C.D..【练习3】:若,)三点都在函数的图象上,则的大小关系为()A.;B.;C.D.考点4:反比例函数的应用例4某种蓄电池的电压为定值,使用此电源时,电流与可变电阻之间的函数关系如图2所示,当用电器的电流为10A时,用电器的可变电阻为_____.【练习4】在一个可以改变容积的密闭容器内,装有一定质量的某种气体,当改变容积时,气体的密度ρ也随之改变.ρ与在一定范围内满足ρ,它的图象如图3所示,则该气体的质量为()A.B.C.D.7.考点5.以反比例函数和一次函数为基架的综合题.例5.如图4,一次函数的图象与反比例函数图象交于A(-2,1)、B(1,n)两点.(1)求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.-3-【练习5】直线y=k1x+b与双曲线y=只有—个交点A(1,2),且与x轴、y轴分别交于B,C两点AD垂直平分OB,垂足为D,(如图5)求直线、双曲线的解析式.【小结】考点课标要求知识与技能目标了解理解掌握灵活应用反比例函数理解反比例函数意义∨会画反比例函数的图象∨理解反比例函数的性质∨能根据实际问题中的反比例关系用待定系数法确定反比例函数的解析式∨∨-4-