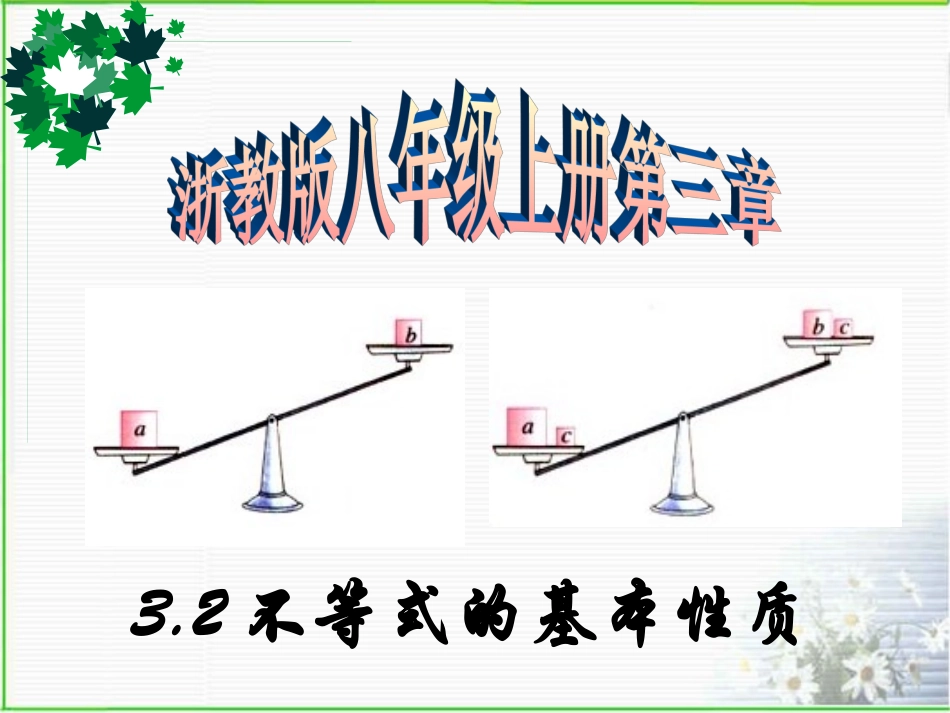
3.2不等式的基本性质1.等式的两边都加上或都减去同一个数或同一个式子,所得的结果仍是等式.2.等式的两边都乘以或都除以同一个不为零的数或式子,所得的结果仍是等式.cba由数轴上a与c的位置关系,你能得出什么结论?你能举几个具体的例子说明吗?(2)若a>b,则a+c与b+c哪个较大?A-c与b-c呢?请分别用数轴上点的位置关系和具体的例子加以说明.(1)已知a
0,则abb+ca+ccc可见,a+c>b+cabb-ca-ccc可见,a-c>b-c你能用数轴上点的位置关系加以说明不等式性质2吗?88____12128×48×4____12×412×48÷48÷4____12÷412÷4<<((––4)4)____((––6)6)((––4)×24)×2____((––6)×26)×2((––4)÷24)÷2____((––6)÷26)÷2<<<<<<<<<<总结为总结为::不等式的两边都乘不等式的两边都乘((或都除以或都除以))同一同一个个正数正数,所得的不等式仍成立;,所得的不等式仍成立;即:如果a>b,且c>0,那么ac>bc,;abcc总结为总结为::不等式的两边都乘以(或除以)同一个不等式的两边都乘以(或除以)同一个负数负数,,必须把必须把不等号的方向改变不等号的方向改变,所得的不等式才成立,所得的不等式才成立..88____12128×(-4)8×(-4)____12×(-4)12×(-4)8÷(-4)8÷(-4)____12÷(-4)12÷(-4)((––4)4)__((––6)6)((––4)×(-2)4)×(-2)__((––6)×(-2)6)×(-2)((––4)÷(-2)4)÷(-2)__((––6)÷(-2)6)÷(-2)>>>>>>>>即:如果a>b,且c<0,那么ac<bc,;>>>>abcc不等式的两边都乘不等式的两边都乘((或都除以或都除以))同一个同一个正数正数,,所得到的不等式仍成立;所得到的不等式仍成立;不等式的两边都乘不等式的两边都乘((或都除以或都除以))同一个同一个负数负数,,必须把必须把不等号的方向改变不等号的方向改变,,所所得到的不等式成立得到的不等式成立..即:如果a>b,且c>0,那么ac>bc,a/c>b/c;如果a>b,且c<0,那么ac<bc,a/c<b/c;想一想:对于不等式a>b,当c=0时,ac___bc,a/c___b/c.=选择适当的不等号填空:(1)0 1,∴aa+1(不等式的基本性质2);(2) 0,∴-2-2(不等式的基本性质2).<<≥≥2(a-1)2(a-1)(5)若-0.5x≤1,两边同乘以-2,得______,(依据___________________)。(4)若2x>-6,两边同除以2,得______,(依据____________________)。(3)若x+1>0,两边同加上-1,得______,(依据:__________________)。x>-1不等式的基本性质2x>-3不等式的基本性质3X≥-2不等式的基本性质3选择适当的不等号,并说明理由1.已知a>b,则a+1b+12.已知a>b,则2a2b3.已知a>b,则-3a-3b4.已知a>b,则-3a+2-3b+25.已知a>b,则4a-34b-3<<>>>>>>•1.若-m>5,则m-5.•2.如果x/y>0,那么xy0.•3.如果a>-1,那么a-b-1-b.•4.-0.9<-0.3,两边都除以(-0.3),得_______.>><,得______.87两边都乘1,x785.3>187x例已知a<0,试比较2a与a的大小。解法一: 2>1,a<0,∴2a<a(不等式的基本性质3).解法二:在数轴上分别表示2a和a的点(a<0),如图.2a位于a的左边,所以2a<a0a2a∣a∣∣a∣想一想:还有其他比较2a与a的大小的方法吗? a<0,∴a+a<a∴2ay,请比较(a-3)x与(a-3)y的大小解:当a>3时,当a=3时,当a<3时,比较等式与不等式的基本性质.例如:等式是否有与不等式的基本性质1类似的传递性?不等式是否有与等式的基本性质类似的移项法则?你可以用列表的方式进行对比.(请与你的伙伴交流)等式不等式基本性质1基本性质2基本性质3若a=b,b=c,则a=c。若a<b,b<c,则a<c。如果a>b,那么a+c>b+c,a-c>b-c如果a=b,那么a+c=b...