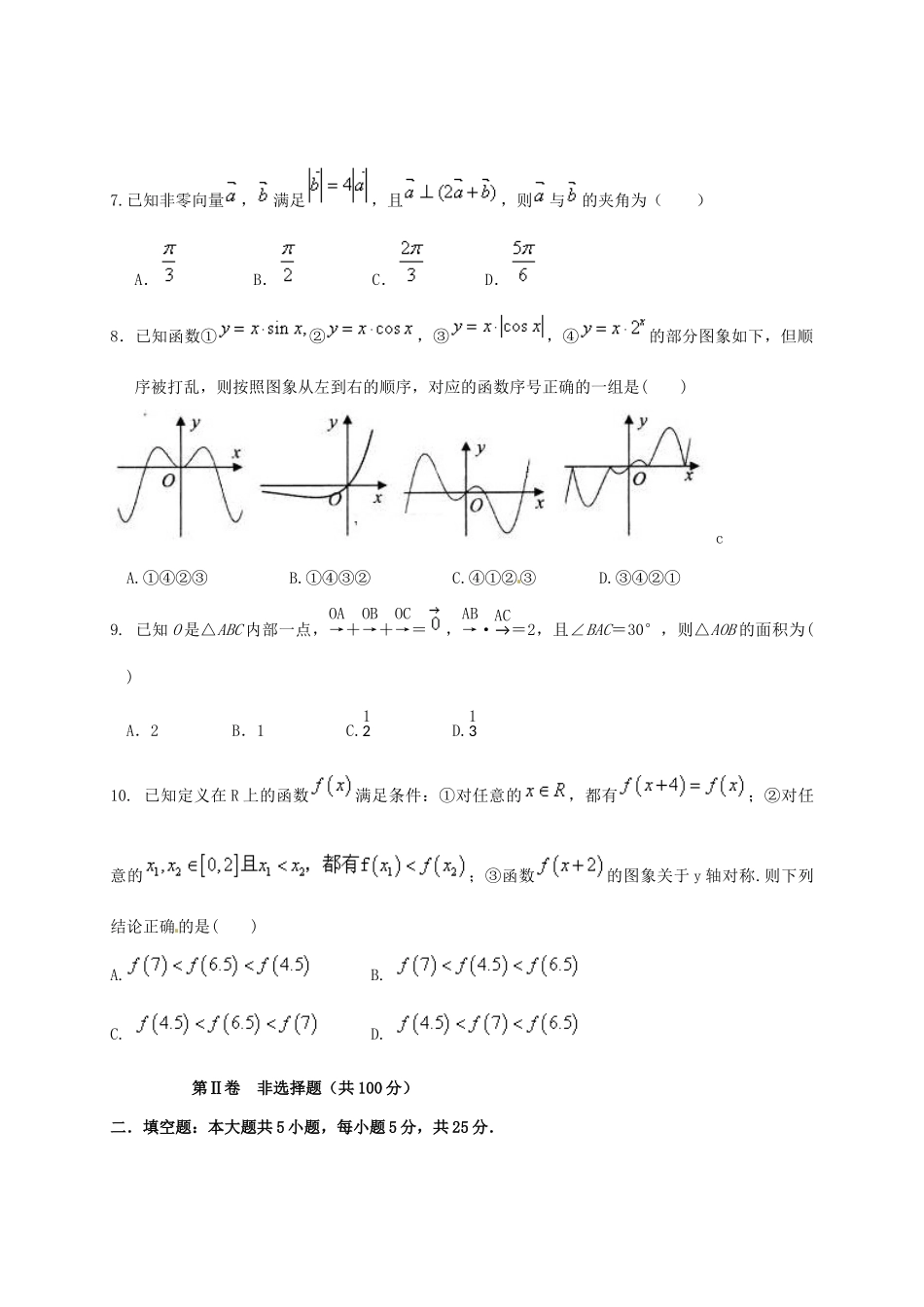
莱芜一中55级高三上学期第一次月考文科数学试题第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求.1.若一复数满足,则()A.B.C.D.2.函数的定义域是()A.B.C.D.3.下列函数中,既是偶函数,且在区间内是单调递增的函数是()A.B.y=cosxC.y=|lnx|D.y=2|x|4.下列有关命题说法正确的是()A.命题“若”的否命题为“若”B.命题“”的否定是“”C.命题“若则”的逆否命题为假命题D.若“p或q”为真命题,则p,q中至少有一个为真命题5.执行程序框图,如果输入的N是6,那么输出的p是()A.120B.720C.1440D.50406.若,则的概率是()A.B.C.D.7.已知非零向量,满足,且,则与的夹角为()A.B.C.D.8.已知函数①②,③,④的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是()cA.①④②③B.①④③②C.④①②③D.③④②①9.已知O是△ABC内部一点,OA→+OB→+OC→=,AB→·AC→=2,且∠BAC=30°,则△AOB的面积为()A.2B.1C.12D.1310.已知定义在R上的函数满足条件:①对任意的,都有;②对任意的;③函数的图象关于y轴对称.则下列结论正确的是()A.B.C.D.第Ⅱ卷非选择题(共100分)二.填空题:本大题共5小题,每小题5分,共25分.11.设单位向量,,满足,则.12.已知,则.13.设函数,则使得成立的的取值范围是.14.已知,,,,根据以上等式归纳出的一般结论是____________.15.给出下列命题:①函数是奇函数;②存在实数,使得;③若,是第一象限角,且,则;④是函数的一条对称轴;⑤函数的图象关于点成中心对称图形.其中正确的序号为.三、解答题:本大题共6小题,共75分16.(满分12分)设命题p:函数f(x)=lg(ax2-4x+a)的定义域为R;命题q:不等式2x2+x>2+ax,对x∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.17.(满分12分)某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组,第2组,第3组,第4组,第5组,得到的频率分布直方图如图所示.(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.18.(满分12分)已知函数.(1)求的定义域及最小正周期;(2)求在区间上的最大值和最小值.19.(满分12分)已知△的面积为,且.(1)求的值;(2)若,,求△ABC的面积.20.(满分13分)已知函数.(1)若函数的图象在处的切线斜率为,求实数的值;(2)在(1)的条件下,求函数的极值;(3)若函数在上是减函数,求实数的取值范围.21.(满分14分)已知函数,(1)求函数的单调区间;(2)求证:;(3)当时,求函数在区间上的最小值.莱芜一中55级高三上学期第一次月考文科数学试题答案一、选择题:1.D2.B3.D4.D5.B6.C7.C8.A9.D10.D二.填空题:11.12.-413.14.15.①④三、解答题:16.解:p:∆<0且a>0,故a>2;q:a>,对x∈(-∞,-1),上恒成立,函数y=在上是增函数所以y<1,故a≥1.“p∨q”为真命题,命题“p∧q”为假命题,等价于p,q一真一假.故1≤a≤217.解:(1)第3组的人数为0.3×100=30,第4组的人数为0.2×100=20,第5组的人数为0.1×100=10.因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:第3组:×6=3;第4组:×6=2;第5组:×6=1.所以应从第3,4,5组中分别抽取3人,2人,1人.(2)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,第5组的1名志愿者为C1.则从6名志愿者中抽取2名志愿者有:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种.其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中的有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C1),(B2,C1),共有9种,所以第4组至少有一名志愿者被抽中的概率为18、解:(1)...