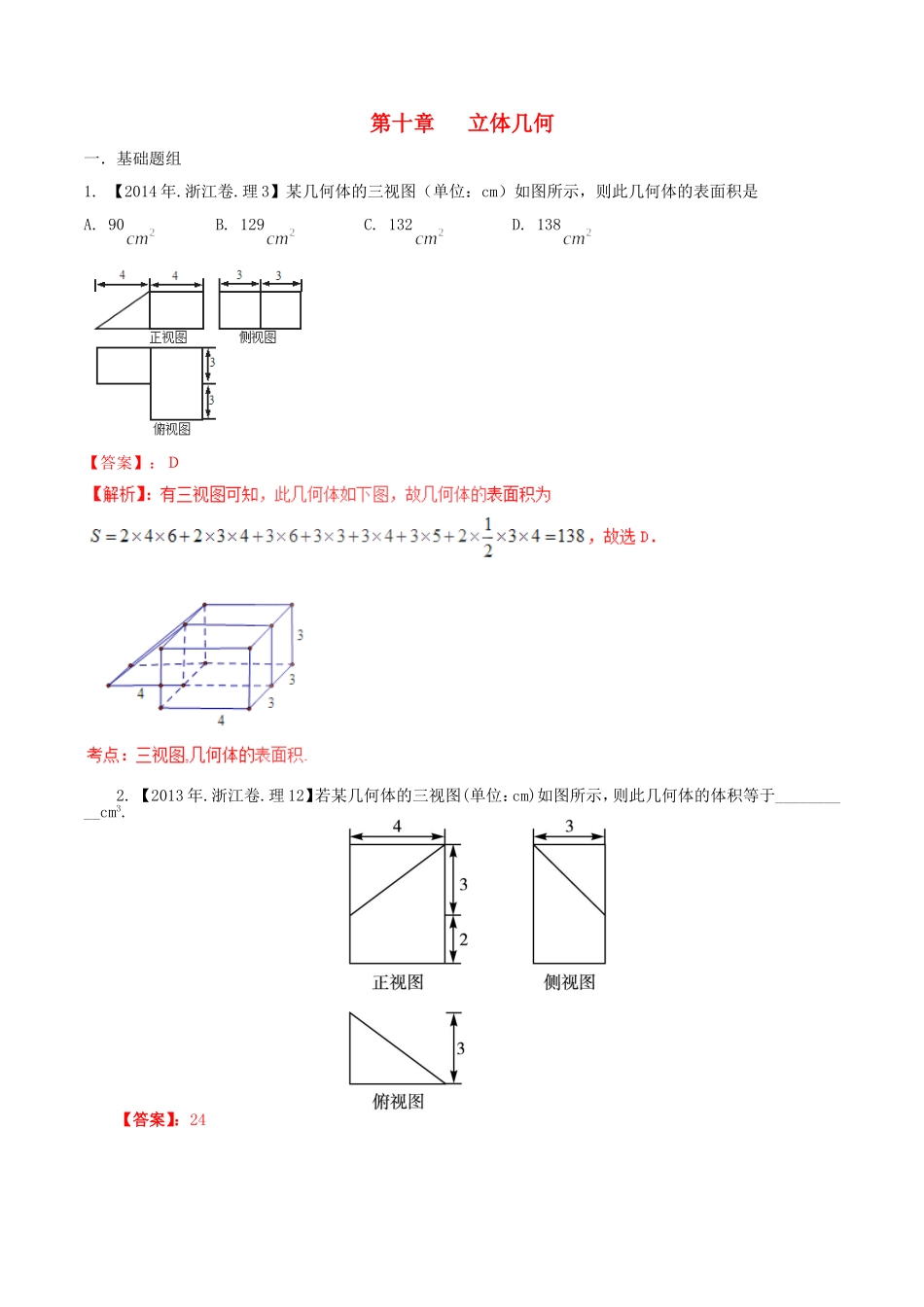
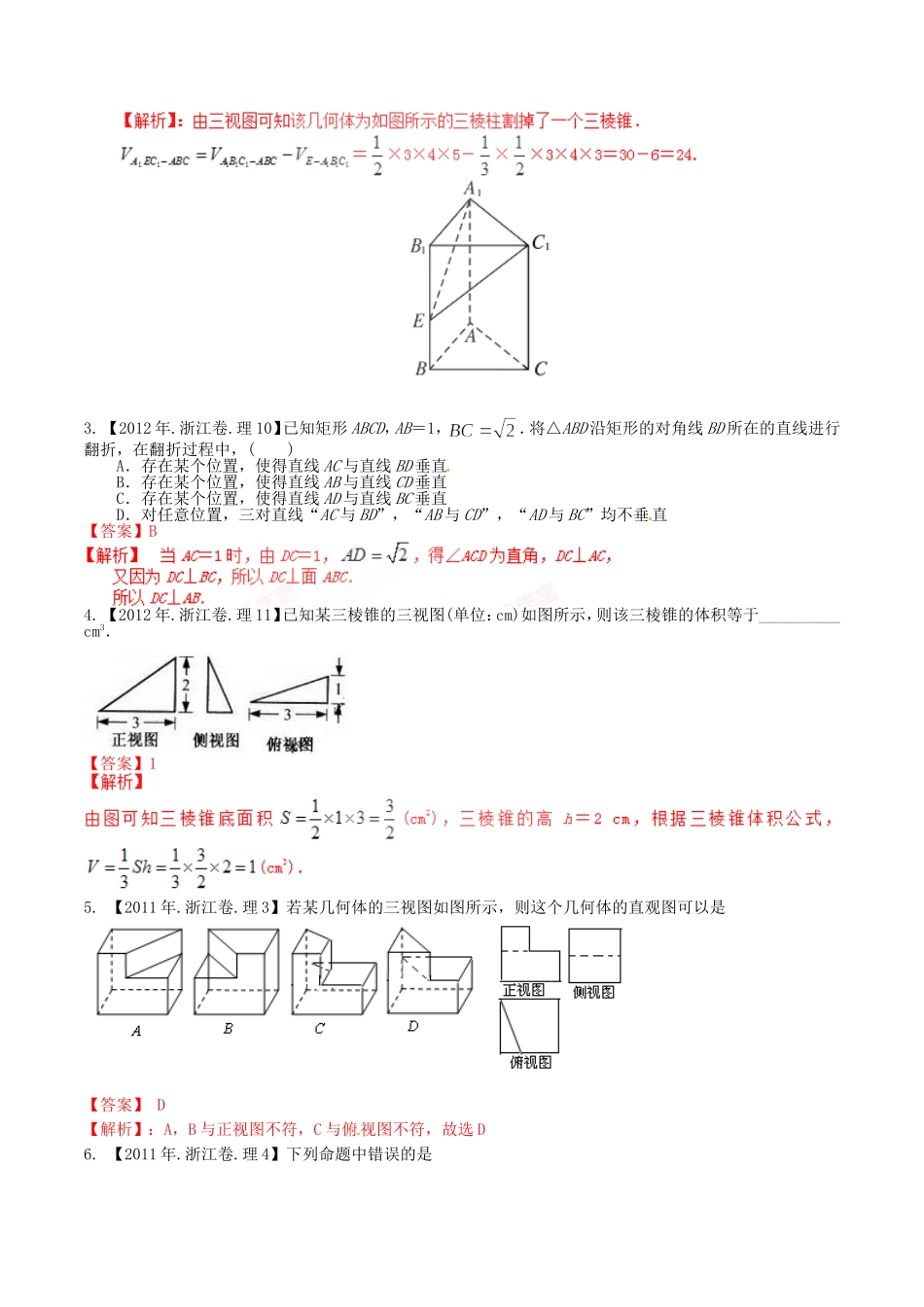
第十章立体几何一.基础题组1.【2014年.浙江卷.理3】某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是A.90B.129C.132D.138【答案】:D2.【2013年.浙江卷.理12】若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于__________cm3.【答案】:243.【2012年.浙江卷.理10】已知矩形ABCD,AB=1,.将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,()A.存在某个位置,使得直线AC与直线BD垂直B.存在某个位置,使得直线AB与直线CD垂直C.存在某个位置,使得直线AD与直线BC垂直D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直【答案】B4.【2012年.浙江卷.理11】已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于__________cm3.【答案】15.【2011年.浙江卷.理3】若某几何体的三视图如图所示,则这个几何体的直观图可以是【答案】D【解析】:A,B与正视图不符,C与俯视图不符,故选D6.【2011年.浙江卷.理4】下列命题中错误的是(A)如果平面,那么平面内一定存在直线平行于平面(B)如果平面不垂直于平面,那么平面内一定不存在直线垂直于平面(C)如果平面,平面,,那么(D)如果平面,那么平面内所有直线都垂直于平面【答案】D7.【2009年.浙江卷.理5】在三棱柱中,各棱长相等,侧掕垂直于底面,点是侧面的中心,则与平面所成角的大小是()A.B.C.D.【答案】:C8.【2009年.浙江卷.理12】若某几何体的三视图(单位:)如图所示,则此几何体的体积是.【答案】:189.【2008年.浙江卷.理14】如图,已知球O点面上四点A、B、C、D,DA平面ABC,ABBC,DA=AB=BC=,则球O点体积等于【答案】10.【2007年.浙江卷.理6】若P是两条异面直线外的任意一点,则(A)过点P有且仅有一条直线与都平行(B)过点P有且仅有一条直线与都垂直(C)过点P有且仅有一条直线与都相交(D)过点P有且仅有一条直线与都异面【答案】B选项D不正确,因为过点P与都异面的直线有数条.故选B.11.【2005年.浙江卷.理6】设、为两个不同的平面,l、m为两条不同的直线,且l,m,有如下的两个命题:①若∥,则l∥m;②若l⊥m,则⊥.那么(A)①是真命题,②是假命题(B)①是假命题,②是真命题(C)①②都是真命题(D)①②都是假命题【答案】D12.【2005年.浙江卷.理12】设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.【答案】90°【解析】:13.【2015高考浙江,理2】某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A.B.C.D.【答案】C.14.【2015高考浙江,理13】如图,三棱锥中,,点分别是的中点,则异面直线,所成的角的余弦值是.【答案】.15.【2015高考浙江,理17】如图,在三棱柱-中,,,,在底面的射影为的中点,为的中点.(1)证明:D平面;(2)求二面角-BD-的平面角的余弦值.【答案】(1)详见解析;(2).【考点定位】1.线面垂直的判定与性质;2.二面角的求解16.二.能力题组1.【2013年.浙江卷.理10】在空间中,过点A作平面π的垂线,垂足为B,记B=fπ(A).设α,β是两个不同的平面,对空间任意一点P,Q1=fβ[fα(P)],Q2=fα[fβ(P)],恒有PQ1=PQ2,则().A.平面α与平面β垂直B.平面α与平面β所成的(锐)二面角为45°C.平面α与平面β平行D.平面α与平面β所成的(锐)二面角为60°【答案】:A∴点Q1与Q2重合于同一点由此可得,四边形PP1Q1P2为矩形,且∠P1Q1P2是二面角α-l-β的平面角 ∠P1Q1P2是直角,∴平面α与平面β垂直,故选A2.【2009年.浙江卷.理17】如图,在长方形中,,,为的中点,为线段(端点除外)上一动点.现将沿折起,使平面平面.在平面内过点作,为垂足.设,则的取值范围是.【答案】:3.【2007年.浙江卷.理16】已知点O在二面角的棱上,点P在内,且.若对于内异于O的任意一点Q,都有,则二面角的取值范围是_____________.【答案】【解析】4.【2006年.浙江卷.理14】正四面体ABCD的棱长为1,棱AB∥平面α,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是.【...