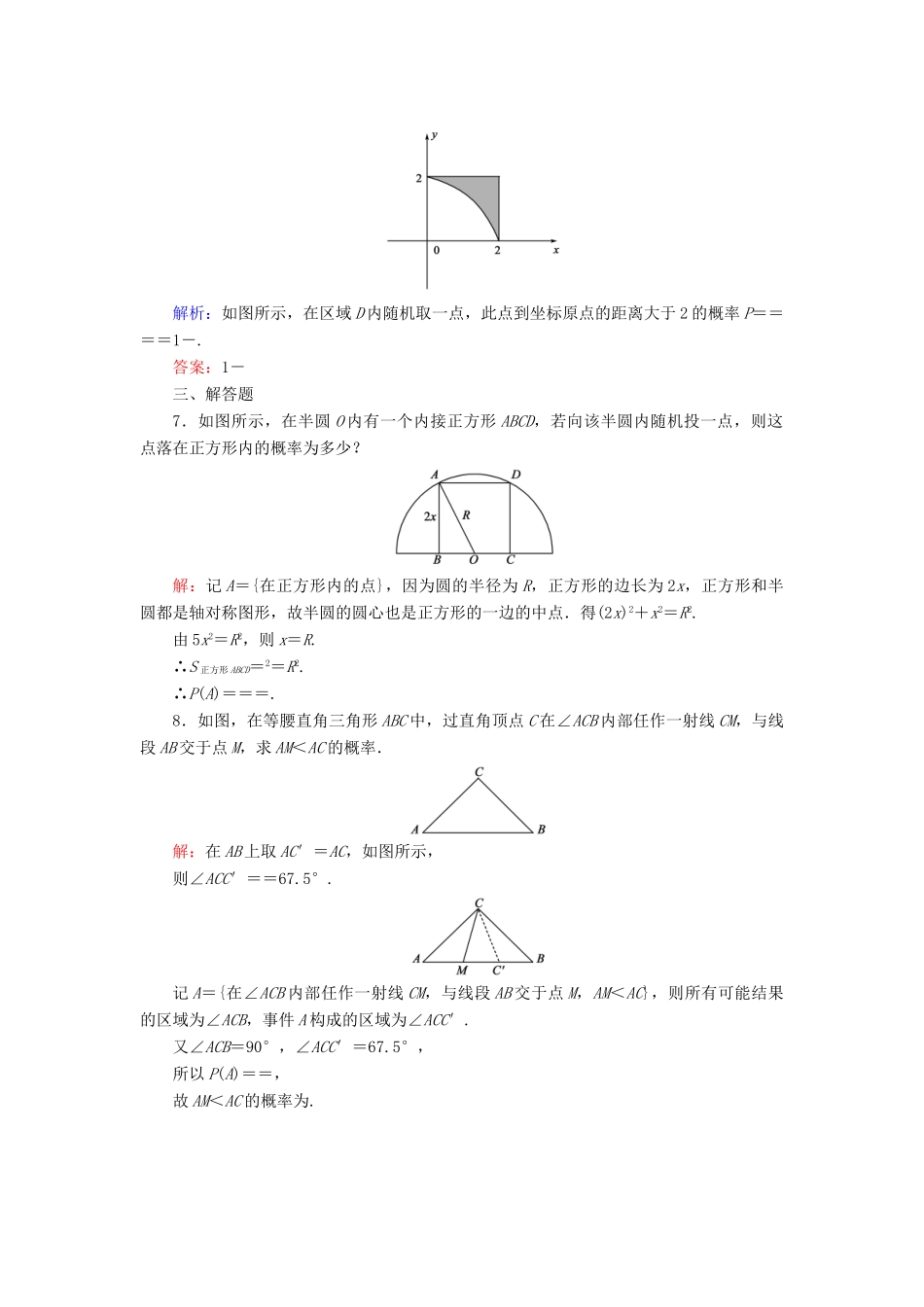
3模拟方法——概率的应用课后拔高提能练一、选择题1.在区间[-1,2]上随机取一个数x,则x∈[0,1]内的概率为()A.B.C.D.解析:选AP==.2.已知某运动员每次投篮命中的概率都为40%.现采用随机模拟的方法估计该运动员三次投篮恰有1次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907966191925271932812458569683431257393027556488730113537989据此估计,该运动员三次投篮恰有1次命中的概率为()A.0.35B.0.40C.0.20D.0.15解析:选B在20组随机数中,恰有一次命中的有925,458,683,257,027,488,730,537共8组,故所求的概率为=0.4.3.如图,设A为圆O上一定点,在圆上任取一点B,则∠AOB<60°的概率为()A.B.C.D.解析:选BP==.二、填空题4.利用计算机产生0~1之间的均匀随机数a,则事件“3a-1<0”发生的概率为________.解析:由3a-1<0,得a<,又0<a<1,∴0<a<,∴事件“3a-1<0”发生的概率P==.答案:5.利用计算机产生0~1之间的均匀随机数a,则使关于x的一元二次方程x2-x+a=0无实根的概率为________.解析:∵关于x的一元二次方程x2-x+a=0无实根,∴判别式Δ=1-4a<0,∴a>.∴所求的概率为P==.答案:6.设不等式组表示的平面区域为D,在区域D内随机取一点,则此点到坐标原点的距离大于2的概率为________.解析:如图所示,在区域D内随机取一点,此点到坐标原点的距离大于2的概率P====1-.答案:1-三、解答题7.如图所示,在半圆O内有一个内接正方形ABCD,若向该半圆内随机投一点,则这点落在正方形内的概率为多少?解:记A={在正方形内的点},因为圆的半径为R,正方形的边长为2x,正方形和半圆都是轴对称图形,故半圆的圆心也是正方形的一边的中点.得(2x)2+x2=R2.由5x2=R2,则x=R.∴S正方形ABCD=2=R2.∴P(A)===.8.如图,在等腰直角三角形ABC中,过直角顶点C在∠ACB内部任作一射线CM,与线段AB交于点M,求AM<AC的概率.解:在AB上取AC′=AC,如图所示,则∠ACC′==67.5°.记A={在∠ACB内部任作一射线CM,与线段AB交于点M,AM<AC},则所有可能结果的区域为∠ACB,事件A构成的区域为∠ACC′.又∠ACB=90°,∠ACC′=67.5°,所以P(A)==,故AM<AC的概率为.