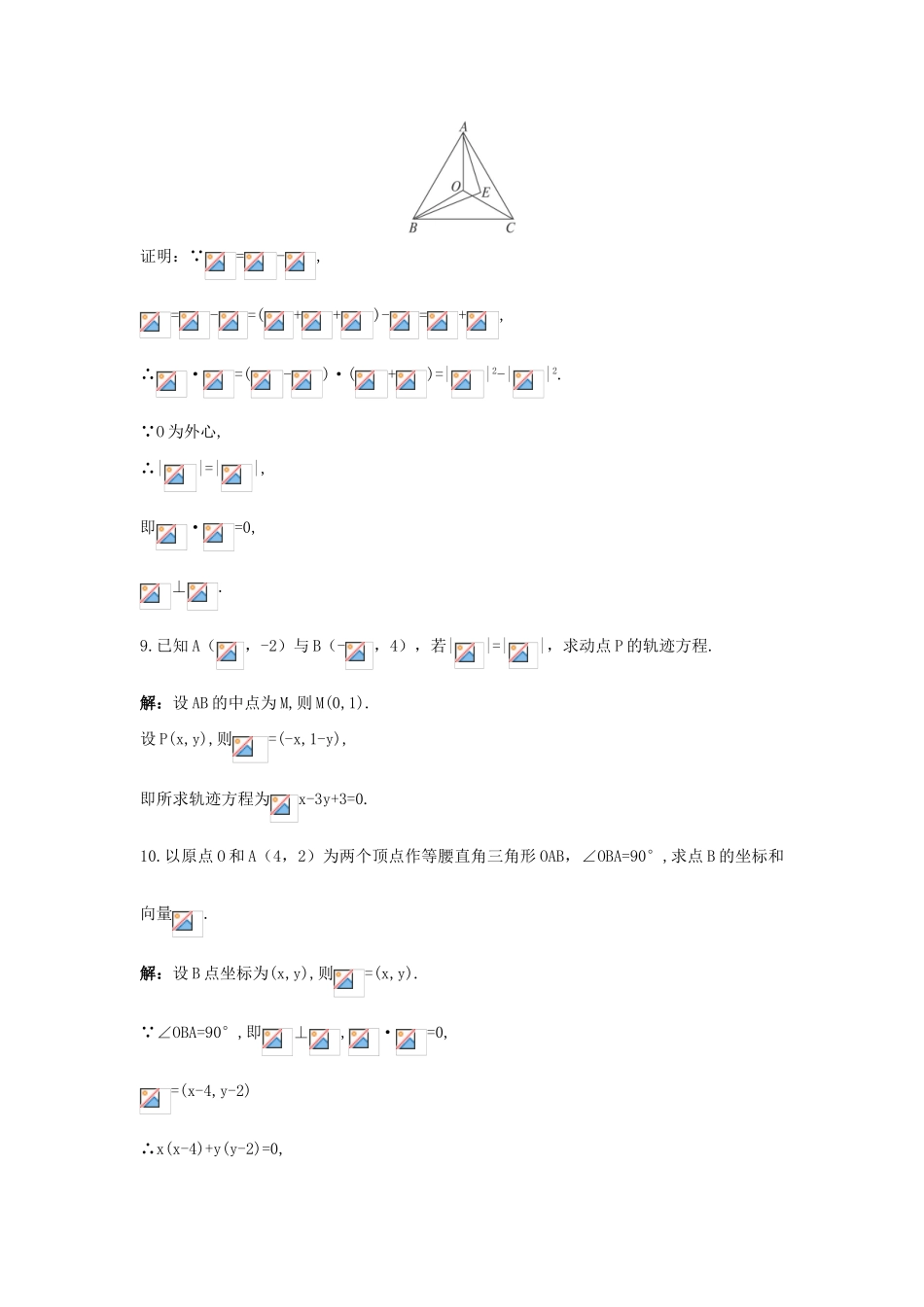
高中数学第2章平面向量2.5向量的应用第一课时成长训练苏教版必修4夯基达标1.在△ABC中,AB=AC,D、E分别是AB、AC的中点,则()A.=B.与共线C.=D.与共线解析:如图,=,∴,共线.答案:D2.在△ABC中,若||=1,||=1,||=1.5,则|-|的值为()A.0B.1C.1.5D.2解析:|-|=||=1.5.答案:C3.若=2e1,=4e1,且与的模相等,则四边形ABCD是()A.平行四边形B.梯形C.等腰梯形D.菱形解析:=,又||=||,∴四边形ABCD为等腰梯形.答案:C4.有一边长为1的正方形ABCD,设=a,BC=b,=c,则|a+b+c|=____________解析:如图,|a+b+c|=2|c|=.答案:5.已知O(0,0)和A(6,3),若点P在直线OA上,且PA=2,P是线段OB的中点,则B的坐标是__________________.解析:设P(x,y),则=(6,3),∴(x,y)=λ(6,3).又=(6-x,3-y),∴(6-x,3-y)=2(x,y).得x=2,y=1,∴B点坐标为(4,2).答案:(4,2)6.过点(-1,3)且垂直于直线x-2y+3=0的直线方程为______________.解析:x-2y+3=0的一个法向量为(1,-2),设P(x,y)是要求直线上任一点,则,即2x+y-1=0.答案:2x+y-1=07.已知Rt△ABC,∠C=90°,设AC=m,BC=n,若D为斜边AB中点,求证CD=AB.解析:以C为坐标原点,以CB、CA所在的直线为x轴、y轴建立坐标系,如图所示.A(0,m),B(n,0),∵D为AB中点,D(,),∴||=,||=.∴||=||,即CD=AB.命题得证.8.如图,O为△ABC的外心,E为三角形内一点,满足=++,求证:⊥.证明:∵=-,=-=(++)-=+,∴·=(-)·(+)=||2-||2.∵O为外心,∴||=||,即·=0,⊥.9.已知A(,-2)与B(-,4),若||=||,求动点P的轨迹方程.解:设AB的中点为M,则M(0,1).设P(x,y),则=(-x,1-y),即所求轨迹方程为x-3y+3=0.10.以原点O和A(4,2)为两个顶点作等腰直角三角形OAB,∠OBA=90°,求点B的坐标和向量.解:设B点坐标为(x,y),则=(x,y).∵∠OBA=90°,即⊥,·=0,=(x-4,y-2)∴x(x-4)+y(y-2)=0,即x2+y2-4x-2y=0.①设OA的中点为C,则点C(2,1).=(2,1),=(x-2,y-1),在等腰Rt△AOB中,⊥,∴2(x-2)+y-1=0,即2x+y-5=0.②解①②得或故B点的坐标为(1,3)或(3,-1).当B(1,3)时,=(-3,1);当B(3,-1)时,=(-1,-3).走近高考11.(经典回放)已知△ABC的三个顶点A、B、C及平面内一点P,且+=,则点P与△ABC的位置关系是()A.P在△ABC内部B.P在△ABC外部C.P在AB边上或其延长线上D.P在AC边上解析:∵=,∴=+=,即=2.∴A、C、P三点共线,即P在AC上.答案:D12.(经典回放)在△ABC中,O为中线AM上的一个动点,若AM=2,则·(+)的最小值是______________.解析:由题意易得=2||·||·cos180°=-2||·||.又||+||=2,∴||·||≤()2=1.(当且仅当||=||时等号成立)∴·()=-2||·||≥-2.即O为AM中点时,取最小值-2.答案:-2