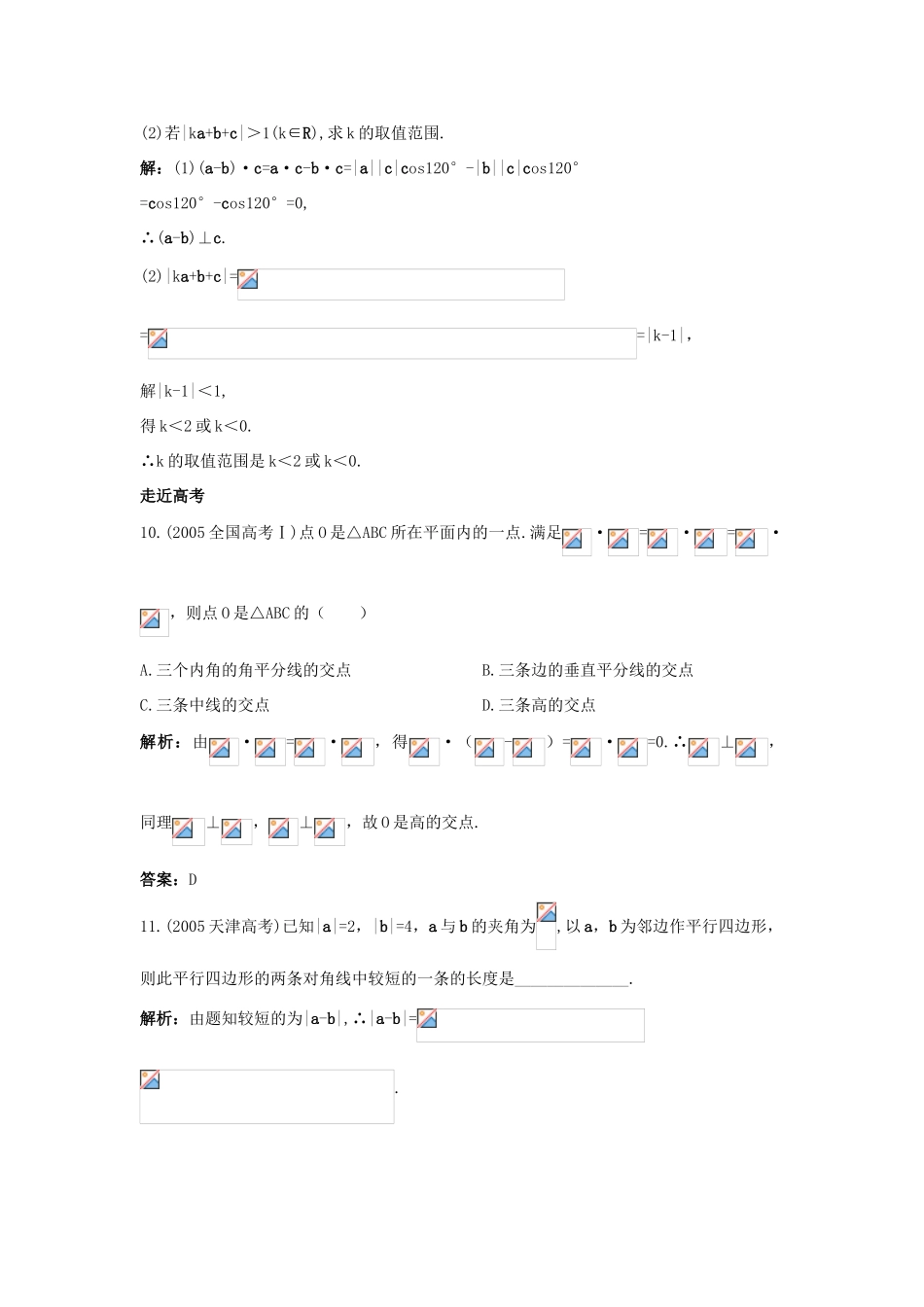
高中数学第2章平面向量2.4向量的数量积第二课时成长训练苏教版必修4夯基达标1.在△ABC中,若=a,=b,=c,且a·b=b·c=c·a,则△ABC的形状是()A.等腰三角形B.直角三角形C.等边三角形D.以上三项均不正确解析:a·b=b·c可得b(a-c)=·()=0,即AC垂直于对应中线,同理可得△ABC三边分别对应垂直于其边上的中线,故△ABC为等边三角形.答案:C2.已知a,b,c为任意向量,m∈R,则下列等式不一定成立的是()A.(a+b)+c=a+(b+c)B.(a+b)·c=a·c+b·cC.m(a+b)=ma+mbD.(a·b)·c=a·(b·c)解析:D项式中,a·b,b·c是数量,而a,c方向也未必一致.所以不一定成立,即向量数量积不满足结合律.答案:D3.向量a,b满足(a-b)·(2a+b)=-4,且|a|=2,|b|=4,则a与b夹角的余弦值等于____________.解析:(a-b)(2a+b)=2a2-b2-a·b=2×22-42-2×4cos〈a,b〉=-4.解得cos〈a,b〉=.答案:4.已知向量a=(1,1),b=(2,-3),若ka-2b与a垂直,则数k等于_______________.解析:因(ka-2b)⊥a,∴(ka-2b)·a=ka2-2a·b=0,即2k-2(2-3)=0,得k=-1.答案:-15.若非零向量a,b满足|a+b|=|a-b|,则a与b所成角的大小为_______________.解析:由|a+b|=|a-b|,得(a+b)2=(a-b)2,即a·b=0,∴a⊥b,于是〈a,b〉=90°.答案:90°6.已知a·b=,|a|=4,a与b的夹角为135°,则|b|=_______________.解析:a·b=|a||b|cos〈a,b〉=4|b|cos135°=-122,解得|b|=6.答案:67.若向量满足a+b+c=0,且|a|=3,|b|=1,|c|=4,则a·b+b·c+c·a=_______________.解析:由a+b+c=0,得c=-a-b,∴a·b+b·c+c·a=a·b+b·c+(-a-b)·a=b·c-a2=-9=|b|·|c|·cos(π-C)-9=-1×4·=4.答案:48.已知|a|=1,|b|=,(1)若〈a,b〉=,求|a+b|;(2)若a与a-b垂直,求a与b的夹角.解:(1)|a+b|==.(2)由a(a-b)=0,得a2=a·b=|a||b|cos〈a,b〉,∴cos〈a,b〉=,∴〈a,b〉=.9.已知平面上三个向量a,b,c的模均为1,它们相互之间的夹角均为120°.(1)求证:(a-b)⊥c;(2)若|ka+b+c|>1(k∈R),求k的取值范围.解:(1)(a-b)·c=a·c-b·c=|a||c|cos120°-|b||c|cos120°=cos120°-cos120°=0,∴(a-b)⊥c.(2)|ka+b+c|===|k-1|,解|k-1|<1,得k<2或k<0.∴k的取值范围是k<2或k<0.走近高考10.(2005全国高考Ⅰ)点O是△ABC所在平面内的一点.满足·=·=·,则点O是△ABC的()A.三个内角的角平分线的交点B.三条边的垂直平分线的交点C.三条中线的交点D.三条高的交点解析:由·=·,得·(-)=·=0.∴⊥,同理⊥,⊥,故O是高的交点.答案:D11.(2005天津高考)已知|a|=2,|b|=4,a与b的夹角为,以a,b为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度是______________.解析:由题知较短的为|a-b|,∴|a-b|=.答案: