柱锥台的表面积与体积VIP免费

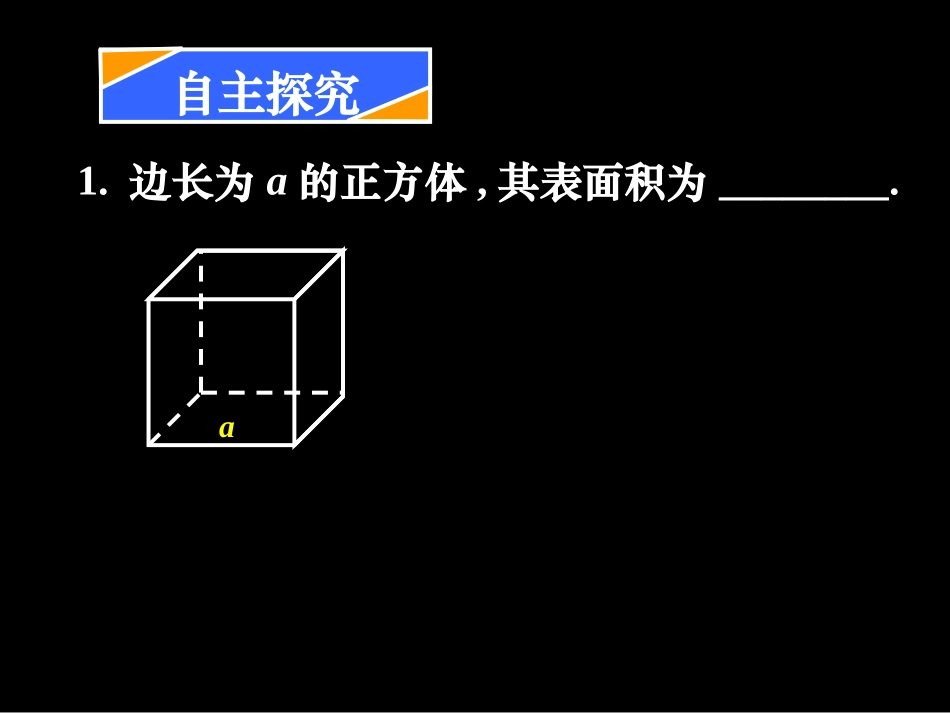
a1.边长为a的正方体,其表面积为________.自主探究1.边长为a的正方体,其表面积为________.26aa自主探究1.边长为a的正方体,其表面积为________.2.长、宽、高分别为a、b、c的长方体,其表面积为_________________.26aaabc自主探究1.边长为a的正方体,其表面积为________.2.长、宽、高分别为a、b、c的长方体,其表面积为_________________.26a2ab+2ac+2bcaabc自主探究在初中学过正方体和长方体的表面积以及展开图,正方体和长方体的展开图与其表面积的关系吗？几何体表面积展开图平面图形面积空间问题平面问题一、棱柱、棱锥、棱台的展开图及表面积的求法：探究：棱柱、棱锥、棱台也是由多个平面图形围成的多面体，它们的展开图是什么?如何计算它们的表面积?S表=S底+S侧棱柱的侧面展开图是什么？如何计算它的表面积？h正棱柱的侧面展开图chS＝直棱柱侧S表=S底+S侧棱锥的侧面展开图是什么？如何计算它的表面积？正棱锥的侧面展开图h'h'侧面展开'21chS＝正棱锥侧S表=S底+S侧棱台的侧面展开图是什么？如何计算它的表面积？正棱台的侧面展开图侧面展开S表=S底+S侧h'h'')'21hccS（＝正棱台侧棱柱、棱锥、棱台都是由多个平面图形围成的几何体，它们的侧面展开图还是平面图形，计算它们的表面积就是计算它的各个侧面面积和底面面积之和．h'h'S表=S底+S侧')'cc21hS＋（＝正棱台c/=0'21chS＝三棱锥c/=cchchS'＝直棱柱h'h'直棱柱、正棱锥、正棱台的侧面积公式之间有什么关系？上底扩大上底缩小①底面积为_______,②侧面积为_______,③表面积为_______.SBCA8234a2334a23aSABC,则它的的三棱锥练习:已知棱长为,各面均为等边三角形a圆柱的侧面展开图是矩形2222()SrrlrrlOOrl2rlSSr2＝长方形圆柱侧二、圆柱、圆锥、圆台的展开图及表面积的求法：圆锥的侧面展开图是扇形r2lOr2()SrrlrrlrlS圆锥侧r2lOrO’'r'2rx'rxrxl''rxrxrlS侧''()()rlxrxrlrxrx'()rlrlr2lOrO’'r'2r圆台的侧面展开图是扇环2'2'()SrrrlrllrrSS)/（＝＝扇环圆台侧lOrO’'rlOOrlOr2222()Srrlrrl2()Srrlrrl2'2'()Srrrlrl圆柱、圆锥、圆台的表面积公式之间有什么关系？上底扩大上底缩小r/=0r/=r1r2h2l1r'1r2r2l练习：看图回答问题____SS圆锥侧圆锥表____SS圆台侧圆台表____SS圆柱侧圆柱表2463116aaa3avaa2shabcabcvcabshlOOrhrv2hs以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为：ShV(S为底面面积，h为高)一般柱体体积也是：ShV其中S为底面面积，h为棱柱的高．三、柱体、椎体、台体的体积的求法：将一个三棱柱按如图所示分解成三个三棱锥，那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系?123123ShV31(其中S为底面面积，h为高)由此可知，棱柱与圆柱的体积公式类似，都是底面面积乘高；棱锥与圆锥的体积公式类似，都是等于底面面积乘高的．31经过探究得知，棱锥是同底等高的棱柱体积的．即棱锥的体积：31圆锥的体积公式：ShV31(其中S为底面面积，h为高)棱台(圆台)的体积公式:hSSSSV)(31其中，分别为上、下底面面积，h为圆台（棱台）的高．SSS'Sxhsshxx'''ssshxxSxhSV'31)31（台xSSxSh'313131''')(3131ssshSSSh'')(3131shssSh)(31''ssssh由于圆台(棱台)是由圆锥(棱锥)截成的，因此可以利用两个锥体的体积差．得到圆台(棱台)的体积公式(过程略)．根据台体的特征，如何求台体的体积？ABABCDCDPSShDCBAPABCDPVVVhSSSS)(31hSSSSV)(31S为底面面积，h为柱体高ShV0SS分别为上、下底面面积，h为台体高ShV31SSS为底面面积，h为锥体高上底扩大上底缩小柱体、锥体、台体的体积公式之间有什么关系？练习：有一堆规格相同的铁制六角螺帽，已知底面是正六边形，边长为12mm，内孔直径为10mm，高为10mm，问六角螺帽的体积是多少？解：六角螺帽的体积是六棱柱的体积与圆柱体积之差，即:10)210(14.3106124322V)(29563mm)(956.23cm【总一总★成竹在胸】1.柱体、椎体、台体的表面积公式；2.柱体、椎体、台体的体积公式；3.台体与柱体和椎体之间的转换关系.