勾股定理的逆定理课件新VIP免费

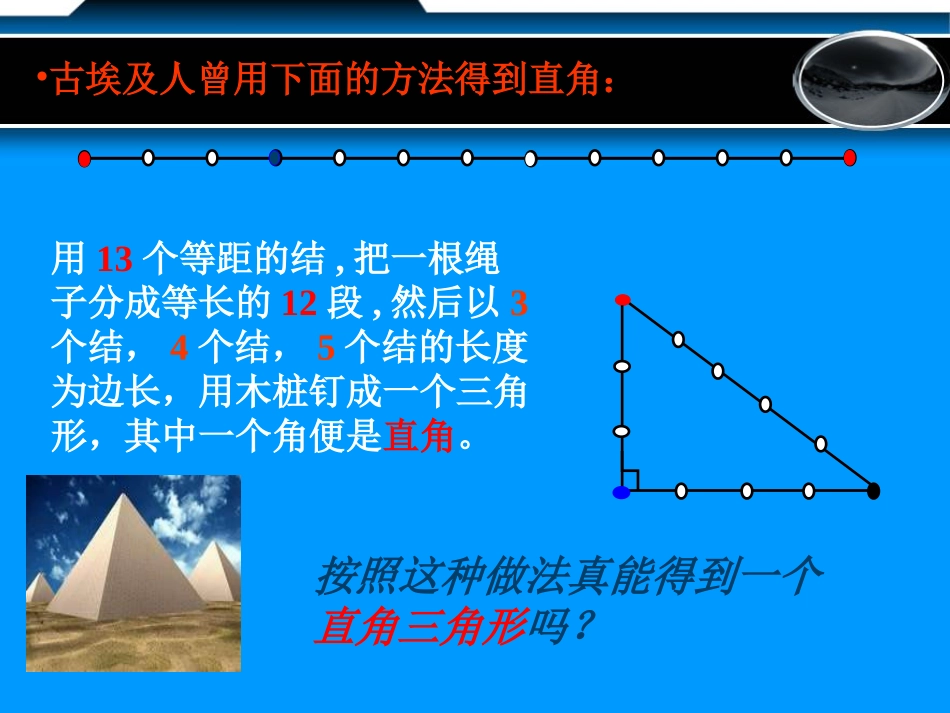
X古埃及人曾用下面的方法得到直角按照这种做法真能得到一个直角三角形吗？•古埃及人曾用下面的方法得到直角：用13个等距的结,把一根绳子分成等长的12段,然后以3个结，4个结，5个结的长度为边长，用木桩钉成一个三角形，其中一个角便是直角。下面的三组数分别是一个三角形的三边长a，b，c：5，12，13；4，7.5，8.5；8，15，17。（1）这三组数都满足222cba吗？（2）它们都是直角三角形吗？如果直角三角形两直角边分别为a，b，斜边为c，那么a2+b2=c2勾股定理如果三角形的三边长a、b、c满足那么这个三角形是直角三角形.a2+b2=c2互逆命题如果三角形的较长边的平方等于其它两条较短边的平方和，那么这个三角形是直角三角形。cabBCA已知：在△ABC中，AB=cBC=aCA=b且a2+b2=c2求证：△ABC是直角三角形证明：画一个△A’B’C’,使∠C’=900,B’C’=a,C’A’=babA’B’C’ ∠C’=900∴A’B’2=a2+b2 a2+b2=c2∴A’B’2=c2∴A’B’=c 边长取正值∴△ABCA’B’C’△（SSS）∴∠C=C’(∠全等三角形对应角相等）∴∠C=900BC=a=B’C’CA=b=C’A’AB=c=A’B’cabBCAabB'C'A'证明:画一个△A’B’C’,使∠C’=900,B’C’=a,C’A’=b在△ABC和△A’B’C’中∴△ABC是直角三角形（直角三角形的定义）勾股定理的逆命题如果直角三角形两直角边分别为a，b，斜边为c，那么a2+b2=c2勾股定理如果三角形的三边长a、b、c满足那么这个三角形是直角三角形。且边C年所对的角为直角.a2+b2=c2互逆命题逆定理定理例1判断由a、b、c组成的三角形是不是直角三角形：(1)a＝15,b＝8,c＝17例题解析(2)a＝13,b＝15,c＝14分析：由勾股定理的逆定理，判断三角形是不是直角三角形，只要看两条较小边的平方和是否等于最大边的平方。解： 152＋82＝225＋64＝289172＝289∴152＋82＝172∴这个三角形是直角三角形下面以a,b,c为边长的三角形是不是直角三角形？如果是那么哪一个角是直角？(1)a=25b=20c=15_________;(2)a=13b=14c=15_________;(4)a:b:c=3:4:5__________;是是不是是∠A=900∠B=900∠C=900(3)a=1b=2c=_________;3像25,20,15,能够成为直角三角形三条边长的三个正整数，称为勾股数.13ABCDABCD34512例1.一个零件的形状如左图所示，按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边尺寸如右图所示，这个零件符合要求吗？例题解析例2.如图，是一块四边形绿地示意图，其中AB长24米，BC长20米，CD长15米，DA长7米，∠C=90度求：绿地ABCD的面积。CCBBAADD242420201515772525例例33：如图，有一块地，已知，：如图，有一块地，已知，AD=4mAD=4m，，CD=3mCD=3m，∠，∠ADC=90°ADC=90°，，AB=13mAB=13m，，BC=12mBC=12m。求这块地的面积。。求这块地的面积。AABBCC334413131212DD2424平方米平方米随堂练习：随堂练习：11、将下列长度的三木棒首尾顺次连接，能组、将下列长度的三木棒首尾顺次连接，能组成直角三角形的是（）成直角三角形的是（）(A)1,2,3(B)4,6,8(C)5,5,4(D)15,12,9(A)1,2,3(B)4,6,8(C)5,5,4(D)15,12,922、如果线段、如果线段aa、、bb、、cc能组成直角三角形能组成直角三角形,,则它们的比可能是（）则它们的比可能是（）（（AA））3:4:7;3:4:7;（（BB））5:12:13;5:12:13;（（CC））1:2:4;1:2:4;（（DD））1:3:5.1:3:5.DDBB3.3.三角形的三边分别是三角形的三边分别是aa、、bb、、c,c,且满足且满足(a+b)(a+b)22-c-c22=2ab,=2ab,则此三角形是则此三角形是:():()A.A.直角三角形直角三角形;B.;B.是锐角三角形是锐角三角形;;3.3.是钝角三角形是钝角三角形;D.;D.是等腰直角三角形是等腰直角三角形..44、已知、已知aa、、bb、、cc为△为△ABCABC的三边的三边,,且满足且满足aa22+b+b22+c+c22++1616==44a+a+b+b+44c.c.试判断△试判断△ABCABC的形状的形状..思维训练思维训练24知识运知识运用用::AAFFEECCBBDD5.5.如图如图::在正方形在正方形ABCDABCD中中,E,E是是BCBC的中点的中点,F,F是是CDCD上一点上一点,,且且CF=CD.CF=CD.猜想△猜想△AEFAEF的形状的形状,,并证明你的结论并证明你的结论..146.6.已知已知a.b.ca.b.c为△为△ABCABC的三边的三边,,且满足且满足aa22cc22––bb22cc22=a=a44–b–b44...