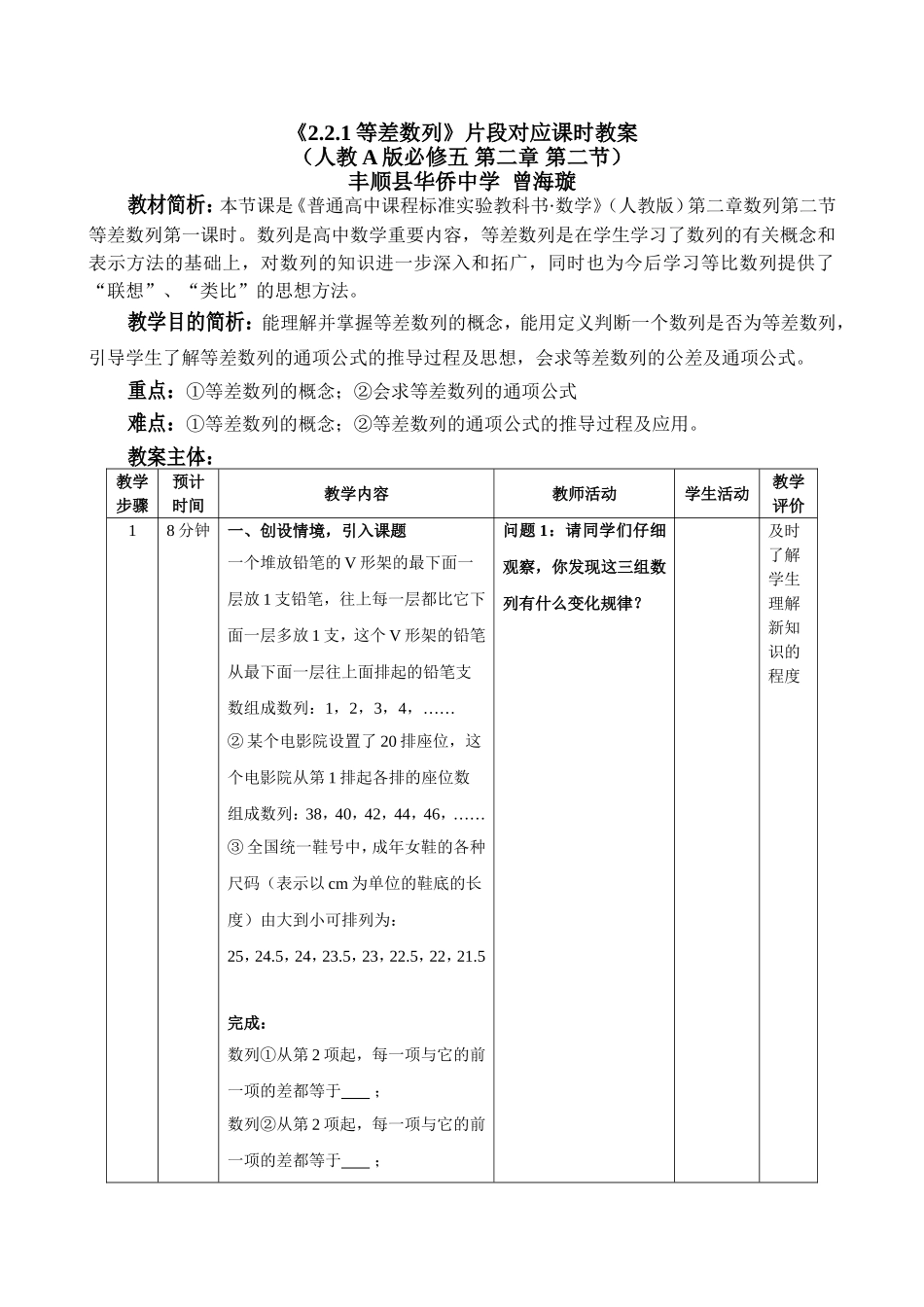
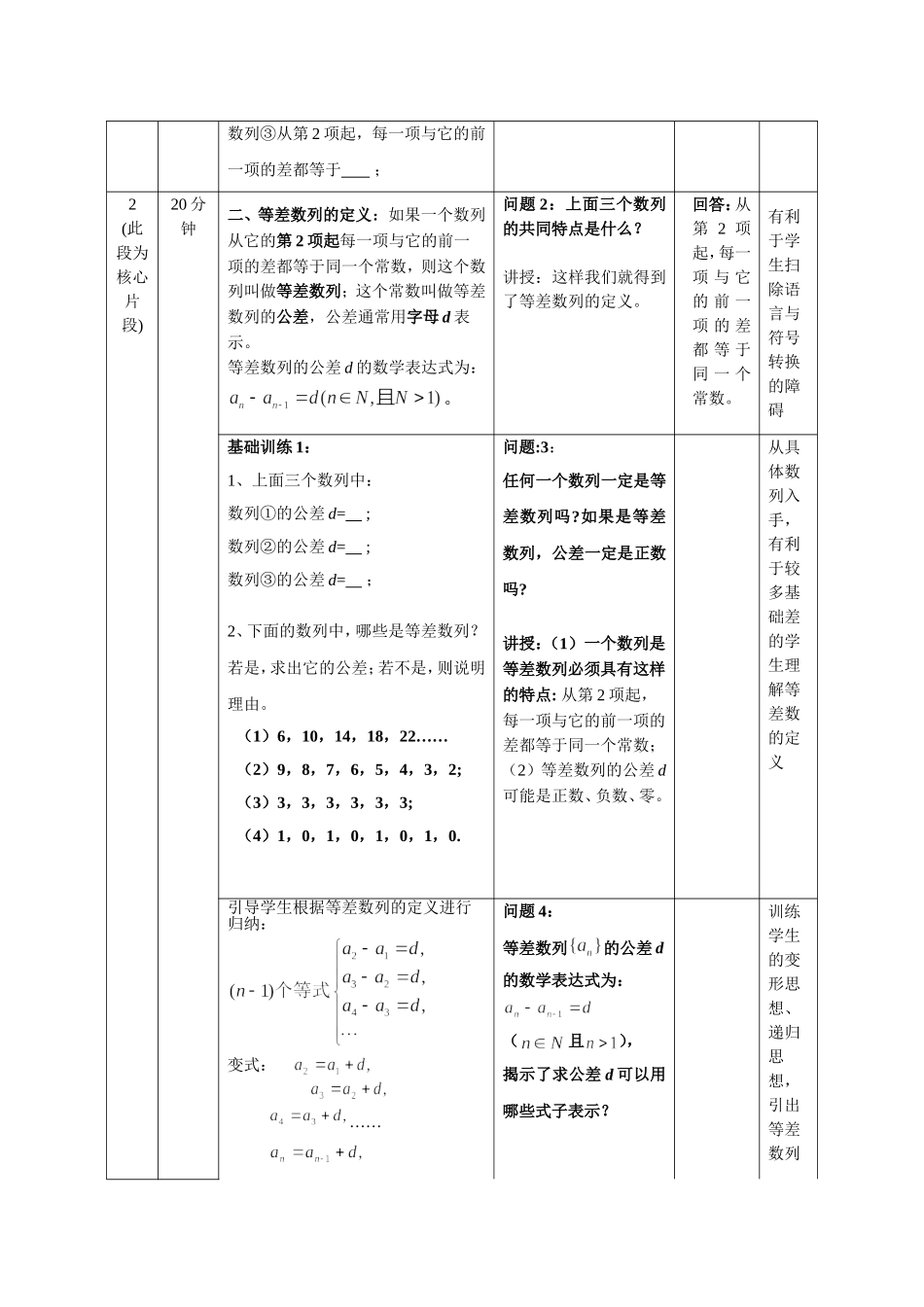
《2.2.1等差数列》片段对应课时教案(人教A版必修五第二章第二节)丰顺县华侨中学曾海璇教材简析:本节课是《普通高中课程标准实验教科书·数学》(人教版)第二章数列第二节等差数列第一课时。数列是高中数学重要内容,等差数列是在学生学习了数列的有关概念和表示方法的基础上,对数列的知识进一步深入和拓广,同时也为今后学习等比数列提供了“联想”、“类比”的思想方法。教学目的简析:能理解并掌握等差数列的概念,能用定义判断一个数列是否为等差数列,引导学生了解等差数列的通项公式的推导过程及思想,会求等差数列的公差及通项公式。重点:①等差数列的概念;②会求等差数列的通项公式难点:①等差数列的概念;②等差数列的通项公式的推导过程及应用。教案主体:教学步骤预计时间教学内容教师活动学生活动教学评价18分钟一、创设情境,引入课题一个堆放铅笔的V形架的最下面一层放1支铅笔,往上每一层都比它下面一层多放1支,这个V形架的铅笔从最下面一层往上面排起的铅笔支数组成数列:1,2,3,4,……②某个电影院设置了20排座位,这个电影院从第1排起各排的座位数组成数列:38,40,42,44,46,……③全国统一鞋号中,成年女鞋的各种尺码(表示以cm为单位的鞋底的长度)由大到小可排列为:25,24.5,24,23.5,23,22.5,22,21.5完成:数列①从第2项起,每一项与它的前一项的差都等于;数列②从第2项起,每一项与它的前一项的差都等于;问题1:请同学们仔细观察,你发现这三组数列有什么变化规律?及时了解学生理解新知识的程度数列③从第2项起,每一项与它的前一项的差都等于;2(此段为核心片段)20分钟二、等差数列的定义:如果一个数列从它的第2项起每一项与它的前一项的差都等于同一个常数,则这个数列叫做等差数列;这个常数叫做等差数列的公差,公差通常用字母d表示。等差数列的公差d的数学表达式为:。问题2:上面三个数列的共同特点是什么?讲授:这样我们就得到了等差数列的定义。回答:从第2项起,每一项与它的前一项的差都等于同一个常数。有利于学生扫除语言与符号转换的障碍基础训练1:1、上面三个数列中:数列①的公差d=;数列②的公差d=;数列③的公差d=;2、下面的数列中,哪些是等差数列?若是,求出它的公差;若不是,则说明理由。(1)6,10,14,18,22……(2)9,8,7,6,5,4,3,2;(3)3,3,3,3,3,3;(4)1,0,1,0,1,0,1,0.问题:3:任何一个数列一定是等差数列吗?如果是等差数列,公差一定是正数吗?讲授:(1)一个数列是等差数列必须具有这样的特点:从第2项起,每一项与它的前一项的差都等于同一个常数;(2)等差数列的公差d可能是正数、负数、零。从具体数列入手,有利于较多基础差的学生理解等差数的定义引导学生根据等差数列的定义进行归纳:变式:……问题4:等差数列的公差d的数学表达式为:(且),揭示了求公差d可以用哪些式子表示?训练学生的变形思想、递归思想,引出等差数列则……的通项,使学生更容易理解通项公式的变形公式三、等差数列的通项公式:由此我们可以猜想得出:以为首项,为公差的等差数列的通项公式为变形公式:(注意不一定大于)问题5:如果等差数列只知道首项,公差d,那么这个数列的其他项如何表示?基础训练2:例1求等差数列5,7,9,11,……的通项公式与第10项。解:因为,所以这个等差数列的通项公式是即。例2数列是等差数列.(1)已知;(2)已知。解:让学生有自主思考的时空。(1),,解得。(2),,解得。35分钟四、总结(1)等差数列的定义:(且)(2)等差数列的通项公式变形公式:45分钟五、思考拓展1、等差数列中,已知、。2、在12和60之间插入3个数,使它们与这两个数成等差数列,求这3个数。52分钟六、作业