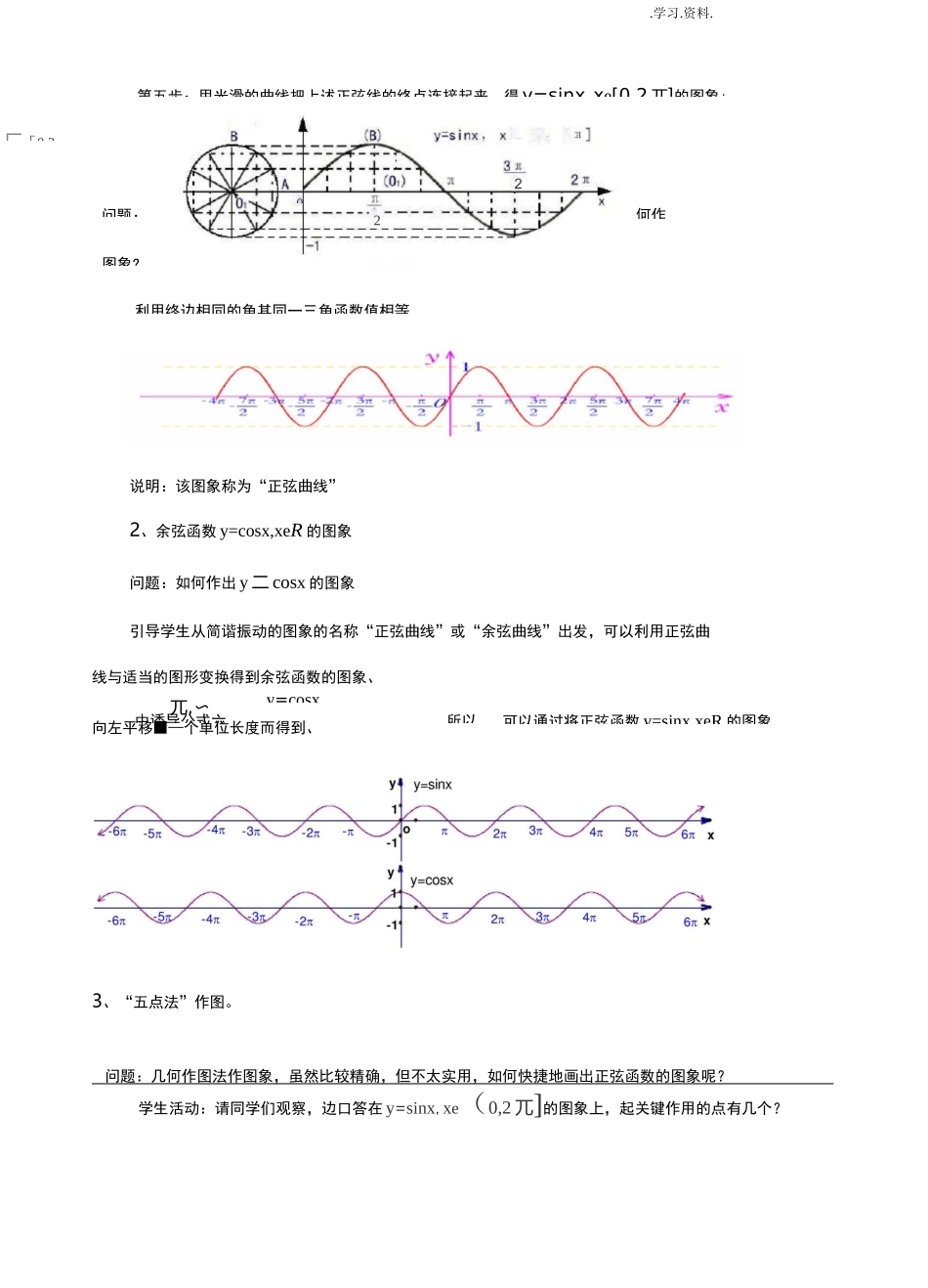
.学习.资料.1.4.1正弦、余弦函数图象的教学设计【教材分析】《正弦函数,余弦函数的图象》是高中新教材人教A版必修四的容,作为函数,它是己学过的一次函数、二次函数、指数函数与对数函数的后继容,是在已有三角函数线知识的基础上,来研究正余弦函数的图象与性质的,它是学习三角函数图象与性质的入门课,是今后研究余弦函数、正切函数的图象与性质、正弦型函数的图象的知识基础和方法准备。因此,本节的学习在全章中乃至整个函数的学习中具有极其重要的地位与作用。本节共分两个课时,本课为第一课时,主要是利用正弦线画出的图象,考察图象的特点,用“五点作图法”画简图,并掌握与正弦函数有关的简单的图象平移变换和对称变换;再利用图象研究正余弦函数的部分性质(定义域、值域等)【学情分析】本课的学习对象为高二下学期的学生,他们经过近一年半的高中学习,已具有一定的学习基础和分析问题、解决问题的能力,思维活跃、想象力丰富、乐于尝试、勇于探索,学习欲望强的学习特点。【教学目标】1、知识与技能(1丿会用单位圆中的三角函数线作出y=sinx,xG[0,2兀]的图象,明确图象的形状;兀(2丿根据关系cosx=sin(x+),作出y=cosx,xGR的图象;2(3)用“五点法”作出正弦函数、余弦函数的简图。2、过程与方法进一步培养合作探究、分析概括,以及抽象思维能力。3、情感态度价值观通过作正弦函数和余弦函数图象,培养认真负责,一丝不苟的学习精神。.学习.资料.【教学重点难点】教学重点:“五点法"画y=sinx,xe[0,2兀],y=cosx,xwli),2兀]图像教学难点:运用几何法画正弦函数图象。【教学过程】一.情景引入实验:简谐振动,得到直观的图象,让学生注意观察它的图形特点,并说明,在物理学中称其为“正弦曲线”或“余弦曲线”.问题:如何得到正弦函数的精确图象?二、新课讲解师:根据以往学习函数的经验,你准备采取什么方法作出正弦函数的图象?作图过程中有什么困难?答:列表、描点、连线。由于表中部分值只能取近似值,再加上描点时的误差,部分同学取的点较少,所以画出的图象难免误差大。如何画出更精确的图象呢?下面我们来学习另一种新的作图方法——几何作图法1.正弦函数的图象利用正弦线作出比较精确的正弦函数y=sinx,xe[0,2兀]图象]先简单复习三角函数线丿第一步:先作单位圆,把O01十二等分;第二步:十二等分后得0,-,-,-,…2兀等角,作出相应的正弦线;632第三步:将x轴上从0到2兀一段分成12等份(2兀^6.28);第四步:取点,平移正弦线,使起点与x轴上的点重合;.学习.资料.由诱导公式六,y=cosx所以,可以通过将正弦函数y=sinx,xeR的图象说明:该图象称为“正弦曲线”2、余弦函数y=cosx,xeR的图象问题:如何作出y二cosx的图象引导学生从简谐振动的图象的名称“正弦曲线”或“余弦曲线”出发,可以利用正弦曲线与适当的图形变换得到余弦函数的图象、兀,〜向左平移■—个单位长度而得到、3、“五点法”作图。问题:几何作图法作图象,虽然比较精确,但不太实用,如何快捷地画出正弦函数的图象呢?学生活动:请同学们观察,边口答在y=sinx,xe(0,2兀]的图象上,起关键作用的点有几个?第五步:用光滑的曲线把上述正弦线的终点连接起来,得y=sinx,xe[0,2兀]的图象;202匚[0,2问题:图象?何作利用终边相同的角其同一三角函数值相等..学习.资料.冗3兀引导学生自然得到下面五个:(0,0),(-,1),(兀,0),(可,一1),(2兀,0)组织学生描出这五个点,并用光滑的曲线连接起来,很自然得到函数的简图,称为“五点法”作图。小结作图步骤:1、列表2、描点3、连线学生小组活动:试试用五点法画出函数y=cosx,xe的图象三、例题分析例1画出下列函数的简图⑴y=1+sinx,x€[0,2n];(2)y=-cosx,x€[0,2n].活动:本例的目的是让学生在教师的指导下会用“五点法”画图,并通过独立完成课后练习1领悟画正弦、余弦函数图象的要领,最终达到熟练掌握.从实际教学来看,“五点法”画图易学却难掌握,学生需练好扎实的基本功.可先让学生按“列表、描点、连线”三步来完成.对学生出现的种种失误,教师不要着急,在学生操作中指导一一纠正,这对以后学习大有好处.解:(1)按五个关键点列表:x0n3...