椭圆的几何性质-高中数学选修-全套课件（人教A版）VIP免费

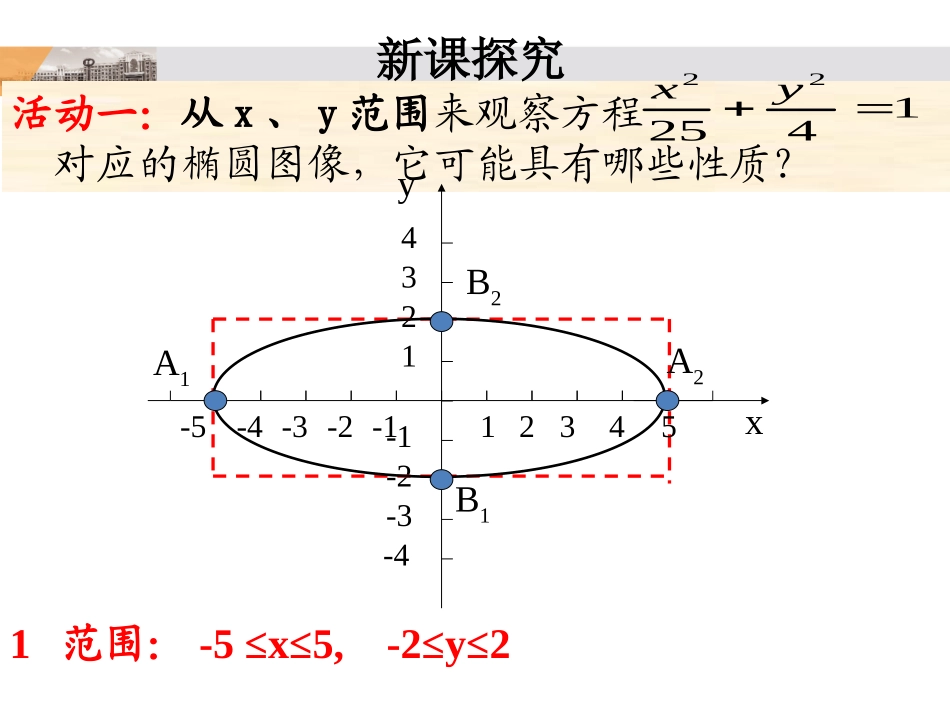
复习回顾1.椭圆定义:平面内与两个定点F1、F2的距离之和为常数（大于|F1F2|）的点的轨迹叫做椭圆。2.椭圆的标准方程：3.椭圆中a,b,c的关系:a2=b2+c2|MF1|+|MF2|=2a（2a>2c）2222+=1>>0xyabab2222+=1>>0xyabba活动一：从x、y范围来观察方程对应的椭圆图像，它可能具有哪些性质？123-1-2-3-44y142522yx12345-1-5-2-3-4xB2A2B1A11范围：-5≤x≤5,-2≤y≤2新课探究活动二：从对称性观察方程对应的椭圆图像，它可能具有哪些性质？123-1-2-3-44y142522yx12345-1-5-2-3-4xB2A2B1A12对称性：椭圆关于x轴、y轴、原点对称P（x，y）2,PxyP3（-x，-y）P1（-x，y）坐标轴是椭圆的两条对称轴，原点是椭圆的对称中心，它的对称中心叫做椭圆的中心。活动三：观察方程对应的椭圆图像，与坐标轴有几个交点，坐标是什么？123-1-2-3-44y142522yx12345-1-5-2-3-4xB2A2B1A13顶点：A1（-5,0）A2（5,0）,B1（0，-2）B2（0，2）活动4：归纳总结)0(12222babyax椭圆简单的几何性质oyB2B1A1A2F1F2x(0,b)(a，0)(0,-b)(-a，0)1、范围：-a≤x≤a,-b≤y≤b2、对称性：椭圆关于x轴、y轴、原点对称。3、顶点：A1（-a,0）A2（a,0）,B1（0，-b）B2（0，b）根据前面所学有关知识画出下列图形123-1-2-3-44y12345-1-5-2-3-4x142522yx（1）B2A2B1A1123-1-2-3-44y12345-1-5-2-3-4x1162522yx（2）B1A2B24、椭圆的离心率离心率：椭圆的焦距与长轴长的比：叫做椭圆的离心率。[1]离心率的取值范围：0bceaa2=b2+c2分层作业：书114页：必做题2、3、选作题4。123-1-2-3-44y12345-1-5-2-3-4xB2A2B1A1*顶点：椭圆与它的对称轴的四个交点，叫做椭圆的顶点。*长轴、短轴：线段A1A2、B1B2分别叫做椭圆的长轴和短轴。a、b分别叫做椭圆的长半轴长和短半轴长。