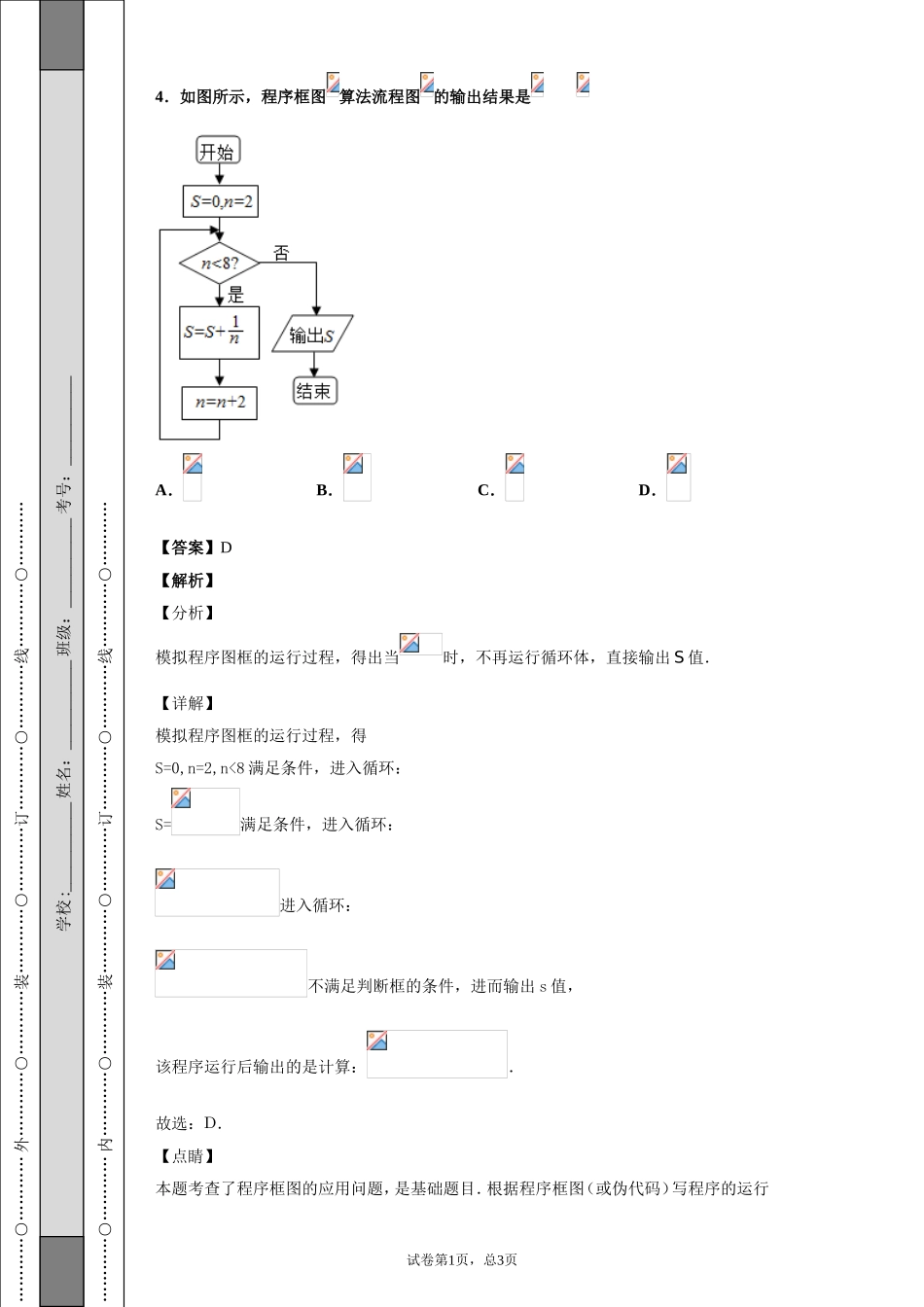
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………绝密★启用前广东省肇庆市2019届高中毕业班第三次统一检测数学(理)试题试卷副标题考试范围:xxx;考试时间:100分钟;命题人:xxx题号一二三总分得分注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(选择题)请点击修改第I卷的文字说明评卷人得分一、单选题1.设集合,,则()A.B.C.D.【答案】C【解析】【分析】解不等式,化简的表示方法,利用集合交集的定义求出.【详解】解: 集合,,∴.故选:C.【点睛】本题考查交集的求法,考查交集定义、不等式性质等基础知识,考查运算求解能力.2.已知为虚数单位,则的值为()A.B.C.D.【答案】A【解析】【分析】试卷第1页,总3页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…………○…………内…………○…………装…………○…………订…………○…………线…………○…………先化简已知的等式,再利用两个复数相等的条件,解方程组求得x的值.【详解】 ∴,∴,即故选A【点睛】本题考查两个复数的乘法法则的应用,以及两个复数相等的条件,基本知识的考查.3.记为等差数列的前项和,公差,,,成等比数列,则()A.-20B.-18C.-10D.-8【答案】D【解析】【分析】由,,成等比数列,可以得到等式,根据等差数列的通项公式可以求出,,代入等式中,这样可以求出的值,最后利用等差数列的前项和公式,求出的值.【详解】解:等差数列的公差,,,成等比数列,可得,即为,解得,则.故选:D.由等比数列的中项性质和等差数列的通项公式和求和公式,计算可得所求和.【点睛】本题考查等差数列的通项公式和求和公式,等比数列中项性质,考查方程思想和运算能力.试卷第1页,总3页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………4.如图所示,程序框图算法流程图的输出结果是A.B.C.D.【答案】D【解析】【分析】模拟程序图框的运行过程,得出当时,不再运行循环体,直接输出S值.【详解】模拟程序图框的运行过程,得S=0,n=2,n<8满足条件,进入循环:S=满足条件,进入循环:进入循环:不满足判断框的条件,进而输出s值,该程序运行后输出的是计算:.故选:D.【点睛】本题考查了程序框图的应用问题,是基础题目.根据程序框图(或伪代码)写程序的运行试卷第1页,总3页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…………○…………内…………○…………装…………○…………订…………○…………线…………○…………结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.5.若,满足约束条件,则的取值范围是()A.B.C.D.【答案】A【解析】【分析】画出可行解域,平移直线,找到在纵轴上截距最大、最小时经过的点,这样可以求出的最大值和最小值,也就求出的取值范围.【详解】解:,满足约束条件,表示的平面区域,如图所示:其中,,由图易得目标函数在处,取最大值2,在处,取得最小值为-2,∴目标函数的取值范围是.故选:A.【点睛】本题考查了求线性目标函...