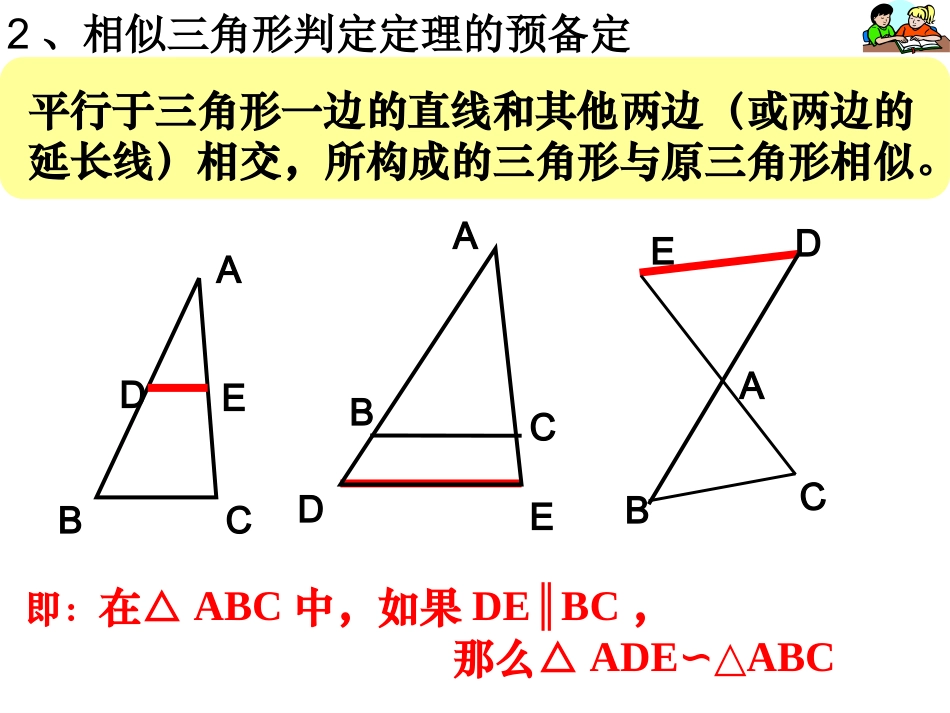
沛河中学九年级沛河中学九年级数学数学董玉坤董玉坤一、知识回顾1、根据相似多边形的定义,你知道什么样的两个三角形相似吗?如果两个三角形满足:(1)对应角相等(2)对应边长度的比相等那么这两个三角形相似.ABCB′C′A′2、相似三角形判定定理的预备定理:DEABCABCDE平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。即:在△ABC中,如果DEBC∥,那么△ADEABC∽△ADBCE相似:相似:相似:相似:ABCA1B1C1角满足:∠A=A∠1,∠B=B∠1,∠C=C∠1,如果:△ABC与△A1B1C1相似,记作△ABC∽△A1B1C1。KCAACCBBCBAAB中与△在△111CBAABC边满足:那么:角满足:∠A=A∠1,∠B=B∠1,∠C=C∠1,角满足:∠A=A∠1,∠B=B∠1,为了方便:如何选择最少的条件使得三角形相似呢:?那么这两个三角形有什么样的关系?探究:下图两个三角形A∠C=C∠1,如果角满足:∠A=A∠1,∠B=B∠1,BCA1B1C11035864二、课堂活动:已知在△ABC和△A′B′C′中.A=A′B=B′∠∠∠∠C=C′∠∠求证:△ABCA′B′C′∽△DEA′B′C′ABC在△ABC的边AB(或延长线)上截取AD=A′B′.过点D作DEBC.∥交AC于点E.则有△ADEABC∽△ ∠ADE=BB=B′∠∠∠∴∠ADE=B′∠又 ∠A=A′AD=A′B′∠∴△ADEA′B′C′≌△(ASA)∴△A′B′C′ABC∽△证明:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。知识要点知识要点相似三角形判定的预备定理ABCDE即:在△ABC中,如果DEBC∥,那么△ADEABC∽△A型你还能画出其他图形吗?平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。探究4相似吗?和△△?较,你们的结论一样吗的结果与邻座的同学比你有发现?把你角形的边长,计算吗?分别度量这两个三它们的第三个角满足,这时,使得和△作△CBAABCCAACCBBCBAABCCBBAACBAABC,,,,ABCA′B′C′如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。两角对应相等,两三角形相似。知识要点知识要点三角形相似三角形相似判定判定定理一定理一A1B1C1ABC△ABC∽△A1B1C1.那么即:如果∠A=∠A1,∠B=∠B1.如果两个三角形有一个内角对应相等,那么这两个三角形一定相似吗?一角对应相等的两个三角形不一定相似。△ACDCBDABC∽△∽△小练习小练习找出图中所有的相似三角形。“双垂直”三角形BDAC有三对相似三角形:△ACDCBD∽△△CBDABC∽△△ACDABC∽△(1)作△ABC和△A’B’C’,使得∠A=∠A’,∠B=∠B’,这时它们的第三个角满足∠C=∠C’吗?(2)分别度量这两个三角形的边长,计算,你有什么发现?,,A'B'A'C'ABACB'C'BC(3)ABC△和△A’B’C’相似吗?ABCA/C/B/分析:要证两个三角形相似,目前只有四个途径。一是三角形相似的定义;二是“平行”定理;三是“三边”定理;四是上节课学习的“两边夹角”定理。ABCA/C/B/已知:在△ABC和△A/B/C/中,//,BBAA求证:ΔABCA∽△/B/C/(把小的三角形移动到大的三角形上)。怎样实现移动呢?为了使用它,就必须创造具备定理的基本图形的条件。怎样创造呢?证明:在ΔABC的边AB、AC上,分别截取AD=A/B/,AE=A/C/,连结DE。ABCA/C/B/P48P48判定定理判定定理33::如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。DE AD=A/B/,A=A∠∠/,AE=A/C/∴ΔADEΔA≌/B/C/(SAS)∴∠ADE=B∠/,又 ∠B/=B∠,∴∠ADE=B∠,∴DE//BC,∴ΔADEΔABC∽。∴ΔA/B/C/ΔABC∽求证:△ABC∽A’B’C’△已知:在△ABC和△A’B’C’,中,若∠A=A’∠,∠B=B’∠,----“两角”定理用数学符号表示:用数学符号表示:例1、已知:ΔABC和ΔDEF中,∠A=400,∠B=800,∠E=800,∠F=600。求证:ΔABCΔDEF∽AFECBD证明: 在ΔABC中,∠A=400,∠B=800,∴∠C=1800-∠A-∠B=1800-400-800=600 在ΔDEF中,∠E=800,∠F=600∴∠B=E∠,∠C=F∠∴ΔABCΔDEF∽(两角对应相等,两三角形相似)。4008008006006060002、课堂练习(1)、已知ΔABC与ΔA/B/C/中,∠B...