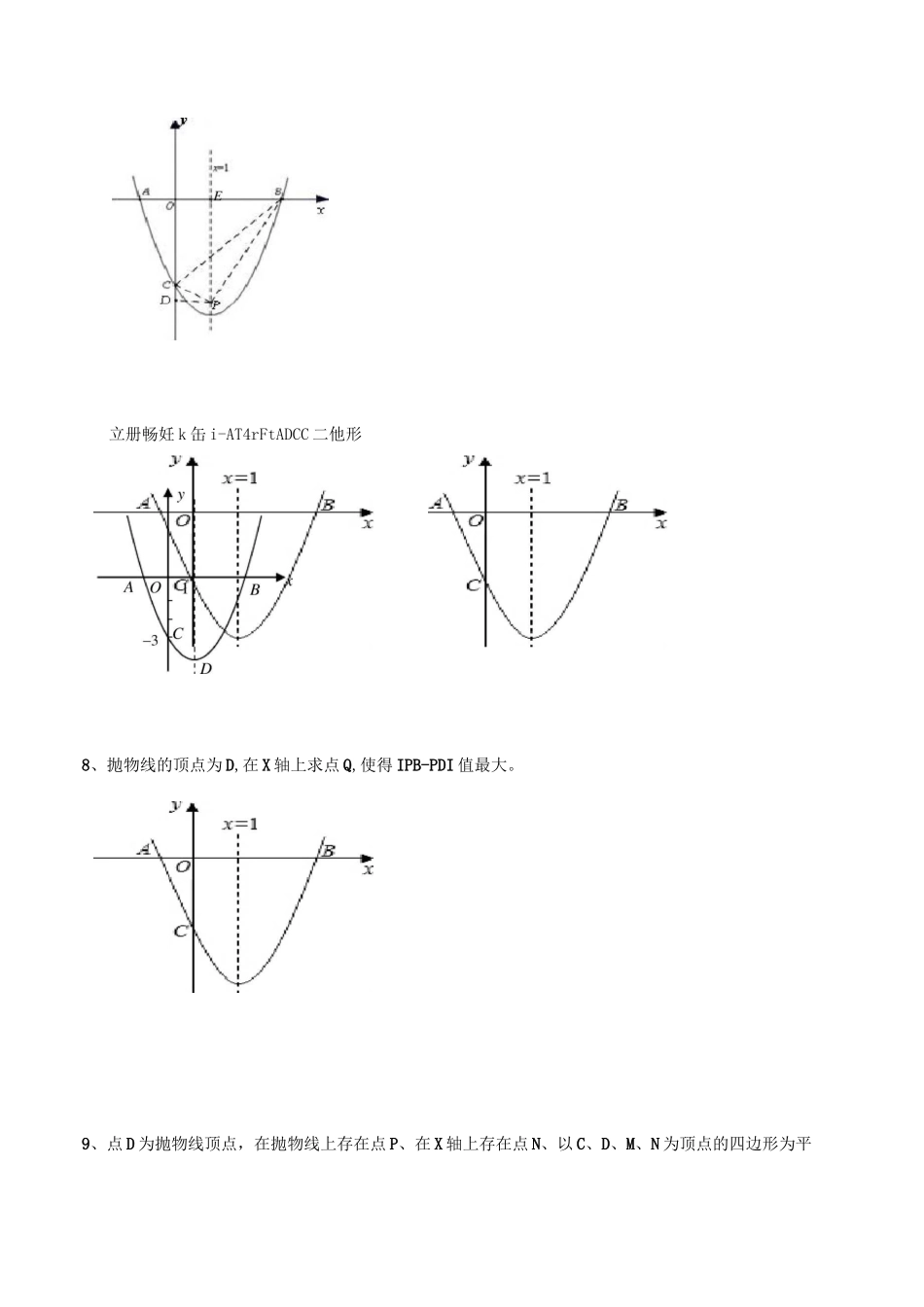
2018年中考数学专题训练之一一、二次函数一题多变如图,已知抛物线y]=ax2+bx+c(a#0)的对称轴为x=1,且抛物线经过A(-1,0)C(0,-3)两点,与x轴交于另一点B•经过点B、C的直线为y2=mx+n。1、求直线BC及抛物线所对应的函数关系式;(用三种方法求抛物线所对应的函数解析式。2、填空:⑴不等式ax2+bx+c〉mx+n的结集为。(2)不等式ax2+bx+c>-3的解集为。⑶当0VxV3时,y的取值范围是o3、在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求此时点M的坐标;4、P是线段BC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;5、P是线段BC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段/PBC面积的最大值;6、设点P为抛物线的对称轴x=1上的一动点,求使ZPCB=90o的点P的坐标.立册畅妊k缶i-AT4rFtADCC二他形8、抛物线的顶点为D,在X轴上求点Q,使得IPB-PDI值最大。9、点D为抛物线顶点,在抛物线上存在点P、在X轴上存在点N、以C、D、M、N为顶点的四边形为平11、在二次函数的图象上是否存在点P,使S沁直=4S,若存在,求出P点的坐标;若不存在,请说明4AMAB行四边形,求出点M的坐标。10、点K(2,m)在抛物线上一点,在抛物线上存在点另一点P,且ZKBP=45°,求点P的坐标.理由;12、将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.13、若点M在线段BA上以每秒1个单位长度的速度从B向A运动(不与A,B重合),同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动.设运动时间为t秒,请写出AMNB的面积S与t的函数关系式,并求出点M运动多少时间时,5MNB的面积最大,最大面积是多少?14、对于(1)中得到的关系式,若x为整数,在使得y为一个完全平方数的相反数的所有x的值中,设x的最大值为m,最小值为n,次小值为s,(注:一个数如果是另一个整数的完全平方,那么就称这个数为完全平方数・)求m、n、s的值•15.抛物线的顶点D,若P为线段BD上的一个动点,过点P作PM丄x轴于点M,求四边形PMAC面积的最大值和此时P点的坐标;16、若P为抛物线在第四象限上的一个动点,过点P作PQIIAC交x轴于点Q.当点P的坐标为时,四边形PQAC是平行四边形;当点P的坐标为时,四边形PQAC是等腰梯形(直接写出结果,不写求解过程).17、⑴设直线y二-x+3与y轴的交点是F,在线段BF上任取一点E(不与B、F重合),经过A,B,E三点的圆交直线BC于点K,试判断△AKF的形状,并说明理由;(2)当E是直线y二-x+3上任意一点时,(2)中的结论是否成立?(请直接写出结论).18、在对称轴上是否存在点M,使AMAC为等腰三角形,若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.19、(1)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;(2)在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.20、点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式;(2)当点P运动到抛物线顶点时,求四边形ABPC的面积;(3)连接PO、PC,并把△POC沿CO翻折,得到四边形POP'C,那么是否存在点P,使四边形POP'C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.21、(1)若点E是x轴上一点,连接CE,且满足ZECB=ZCBD,求点E坐标.(2)若点P在x轴上且位于点B右侧,点A、Q关于点P中心对称,连接QD,且ZBDQ=45°,求点P坐标22、M为CB的中点,ZPMQ在CB的同侧以M为中心旋转,且ZPMQ=45°,MP交y轴于点D,MQ交x轴于点E.设CD的长为m(m>0),BE的长为n,求n和m之间的函数关系式.23.如图,二次函数y二ax2+bx+c(a丰0)的图象,经过点B、C的一次函数为Y=mx+n。12定义函数f:“当自变量X任取一值时,X对应的函数值分别为y或y2,若¥严2,函数f的函数值等于y、y中的较小值;若y=y,函数f的函数值等于y(或y).”当直线Y=kx-5(k2>0)与函数f的图象1212123只有两个交点时,求k的值.