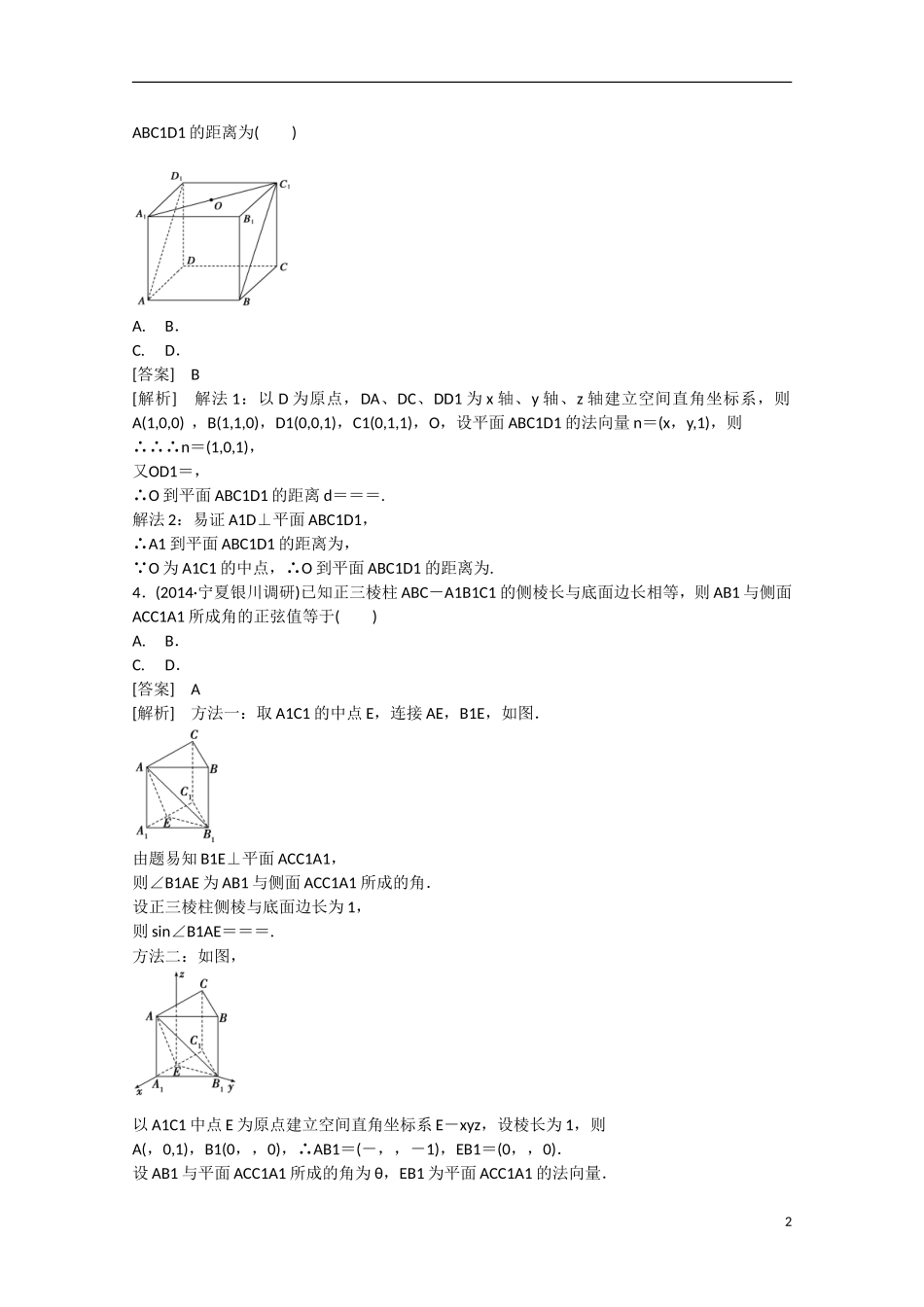
【走向高考】2016届高三数学一轮基础巩固第9章第8节用向量方法求角与距离(理)新人教B版一、选择题1.已知正方体ABCD-A1B1C1D1,则直线BC1与平面A1BD所成的角的余弦值是()A.B.C.D.[答案]C[解析]如图,以D为坐标原点,直线DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系,设正方体棱长为1,则D(0,0,0),A1(1,0,1),B(1,1,0),C1(0,1,1),∴DA1=(1,0,1),DB=(1,1,0),BC1=(-1,0,1),设平面A1BD的一个法向量为n=(x,y,z),则∴∴令x=1得,n=(1,-1,-1),设直线BC1与平面A1BD所成角为θ,则sinθ=|cos〈BC1,n〉|===,∴cosθ==.2.(2014·河北石家庄模拟)在正三棱柱ABC-A1B1C1中,已知AB=2,CC1=,则异面直线AB1和BC1所成角的正弦值为()A.1B.C.D.[答案]A[解析]设线段A1B1,AB的中点分别为O,D,则OC1⊥平面ABB1A1,以OB1,OC1,OD的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,如图,则A(-1,0,),B1(1,0,0),B(1,0,),C1(0,,0),∴AB1=(2,0,-),BC1=(-1,,-),因为AB1·BC1=(2,0,-)·(-1,,-)=0,所以AB1⊥BC1,即异面直线AB1和BC1所成角为直角,则其正弦值为1,故选A.3.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则点O到平面1ABC1D1的距离为()A.B.C.D.[答案]B[解析]解法1:以D为原点,DA、DC、DD1为x轴、y轴、z轴建立空间直角坐标系,则A(1,0,0),B(1,1,0),D1(0,0,1),C1(0,1,1),O,设平面ABC1D1的法向量n=(x,y,1),则∴∴∴n=(1,0,1),又OD1=,∴O到平面ABC1D1的距离d===.解法2:易证A1D⊥平面ABC1D1,∴A1到平面ABC1D1的距离为, O为A1C1的中点,∴O到平面ABC1D1的距离为.4.(2014·宁夏银川调研)已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦值等于()A.B.C.D.[答案]A[解析]方法一:取A1C1的中点E,连接AE,B1E,如图.由题易知B1E⊥平面ACC1A1,则∠B1AE为AB1与侧面ACC1A1所成的角.设正三棱柱侧棱与底面边长为1,则sin∠B1AE===.方法二:如图,以A1C1中点E为原点建立空间直角坐标系E-xyz,设棱长为1,则A(,0,1),B1(0,,0),∴AB1=(-,,-1),EB1=(0,,0).设AB1与平面ACC1A1所成的角为θ,EB1为平面ACC1A1的法向量.2则sinθ=|cos〈AB1,EB1〉|=||=.5.(2014·福建泉州二模)设正方体ABCD-A1B1C1D1的棱长为2,则点D1到平面A1BD的距离是()A.B.C.D.[答案]D[解析]建立如图所示的空间直角坐标系,则D1(0,0,2),A1(2,0,2),D(0,0,0),B(2,2,0),∴D1A1=(2,0,0),DA1=(2,0,2),DB=(2,2,0),设平面A1BD的法向量为n=(x,y,z),则令x=1,则n=(1,-1,-1),∴点D1到平面A1BD的距离是d===.[点评]可用等积法求解VD1-A1BD=VB-A1DD1.一、空间的距离1.两点间的距离:连结两点的线段的长度.2.点到直线的距离:从直线外一点向直线引垂直相交的直线,点到垂足之间线段的长度.3.点到平面的距离:从平面外一点向平面引垂线,点到垂足间线段的长度.连接平面α外一点与平面α内任一点的线段中,垂线段最短.4.平行直线间的距离:从两条平行线中一条上任意取一点向另一条直线引垂线,这点到垂足间线段的长度.5.异面直线间的距离:两条异面直线的公垂线夹在这两条异面直线间的线段的长度.6.直线与平面间的距离:如果一条直线和一个平面平行,从直线上任意一点向平面引垂线,这点到垂足间线段的长度.7.两平行平面间的距离:两个平面的公垂线段的长度.二、求距离的方法1.综合几何方法①找出或作出有关距离的图形;②证明它符合定义;③在平面图形内计算.空间中各种距离的计算,最终都要转化为线段长度,特殊情况也可以利用等积法.2.向量法3(1)求直线到平面的距离设直线a∥平面α,A∈a,B∈α,n是平面α的法向量,过A作AC⊥α,垂足为C,则AC∥n, AB·n=(AC+CB)·n=AC·n,∴|AB·n|=|AC|·|n|.∴直线a到平面α的距离d=|AC|=.(2)求两平行平面间的距离①用公式d=求,n为两平行平面的一个法向量,A、B分别为两平面上的任意两点.②转化为点面距或线面距求解.(3)求点面距时,平面内的点可以任意选取,实际解题...