立体几何中的向量方法习题课VIP免费

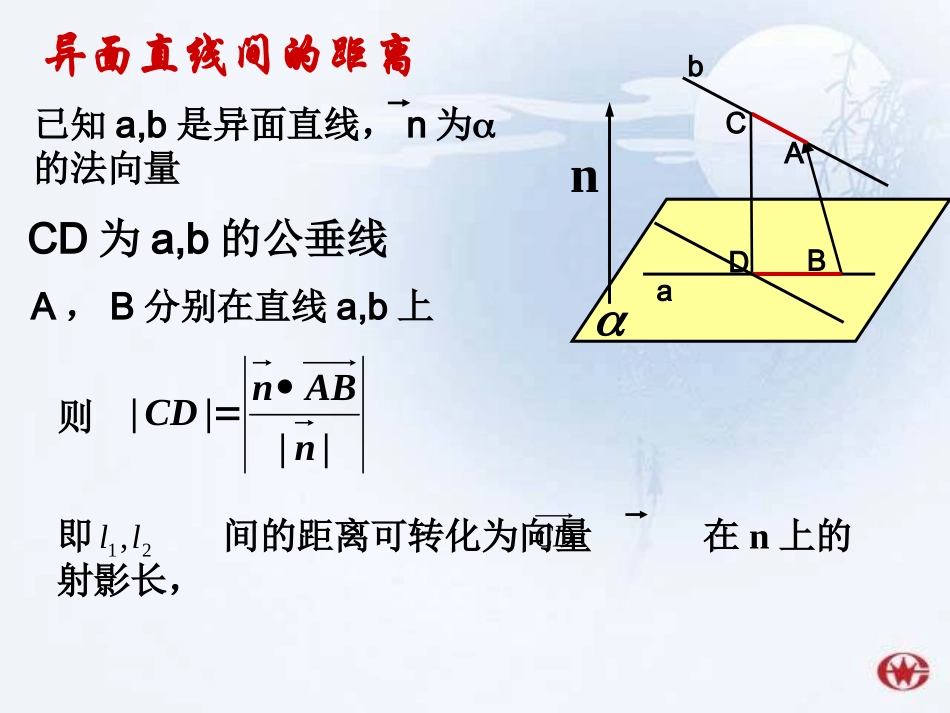
1．如图3-5，已知两条异面直线所成的角为θ，在直线a、b上分别取E、F，已知A’E=m，AF=n，EF=l，求公垂线AA′的长d.EFEAAAAF�解：22()EFEAAAAF�2222()EAAAAFEAAAEAAFAAAF�当E,F在公垂线同一侧时取负号当d等于0是即为“余弦定理”,AAEAAAAF�<>=π—θ（或θ），AFEA,22222lEAAAAFEAAF��2222cosmdnmn2222cosdlmnmnnabCDABCD为a,b的公垂线则||||nABnCDA，B分别在直线a,b上已知a,b是异面直线，n为的法向量异面直线间的距离即间的距离可转化为向量在n上的射影长，21,llCD111101.4,,2,90,ABCABCAAABCACBCBCAEABCEAB例已知：直三棱柱的侧棱底面中为的中点。求与的距离。zxyABCC1).4,2,0(),0,0,2(),0,1,1(),0,0,0(,1BAECxyzC则解：如图建立坐标系),4,2,2(),0,1,1(1BAEC则的公垂线的方向向量为设).,,(,1zyxnBAEC001BAnECn即04220zyxyx取x=1,则y=-1,z=1,所以)1,1,1(n).0,0,1(,,ACAC在两直线上各取点.332||||1nACndBAEC的距离与EA1B1xyzABCDE2、如图，四面体DABC中，AB，BC，BD两两垂直，且AB=BC=2，点E是AC中点；异面直线AD与BE所成角为，且，求四面体DABC的体积。10cos103、在如图的实验装置中，正方形框架的边长都是1，且平面ABCD与平面ABEF互相垂直。活动弹子M，N分别在正方形对角线AC和BF上移动，且CM和BN的长度保持相等，记CM=BN=（1）求MN的长；（2）a为何值时？MN的长最小？（3）当MN的长最小时，求面MNA与面MNB所成二面角的余弦值。(02).aaABCDEFMNa4、如图6，在棱长为的正方体中，分别是棱AB,BC上的动点，且。（1）求证：；（2）当三棱锥的体积取最大值时，求二面角的正切值。''''CBAOOABCBFAEECFA''BEFB'BEFB'FE、O’C’B’A’OABCEF图6O’C’B’A’OABCEF图65、如图，平行六面体中，底面ABCD是边长为a的正方形，侧棱的长为b,且求（1）的长；（2）直线与AC夹角的余弦值。ABCDABCDAA0120.AABAADACBDABCDABCD